Advertisements
Advertisements
Question
A solid cone of radius r and height h is placed over a solid cylinder having same base radius and height as that of a cone. The total surface area of the combined solid is `pir [sqrt(r^2 + h^2) + 3r + 2h]`.
Options
True
False
Solution
This statement is False.
Explanation:
When a solid cone is placed over a solid cylinder of same base radius, the base of cone and top of the cylinder will not be covered in total surface area.
Since the height of cone and cylinder is same,
We get,
Total surface area of cone = πrl + πr2, where r = base radius and l = slant height
Total surface area of shape formed = Total surface area of cone + Total surface area of cylinder – 2(Area of base)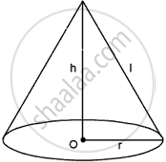
Total surface area of cylinder = 2πrh + 2πr2h, where r = base radius and h = height
= πr(r + l) + (2πrh + 2πr2) – 2(πr2)
= πr2 + πrl + 2πrh + 2πr2 – 2πr2
= πr(r + l + h)
= `pi"r"("r" + sqrt("r"^2 + "h"^2) + 2"h")`
APPEARS IN
RELATED QUESTIONS
From a solid cylinder of height 2.8 cm and diameter 4.2 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid [take π=22/7]
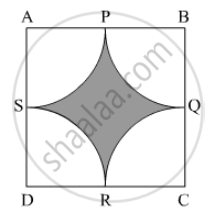
Find the area of the shaded region in Fig. 3, where arcs drawn with centres A, B, C and D intersect in pairs at mid-points P, Q, R and S of the sides AB, BC, CD and DA respectively of a square ABCD of side 12 cm. [Use π = 3.14]
A bucket has top and bottom diameter of 40 cm and 20 cm respectively. Find the volume of the bucket if its depth is 12 cm. Also, find the cost of tin sheet used for making the bucket at the rate of Rs. 1.20 per dm2 . (Use π = 3.14)
A bucket made of aluminum sheet is of height 20cm and its upper and lower ends are of radius 25cm an 10cm, find cost of making bucket if the aluminum sheet costs Rs 70 per
100 cm2
Find the number of metallic circular discs with 1.5 cm base diameter and of height 0.2 cm to be melted to form a right circular cylinder of height 10 cm and diameter 4.5 cm .
The inner and outer radii of a hollow cylinder are 15 cm and 20 cm, respectively. The cylinder is melted and recast into a solid cylinder of the same height. Find the radius of the base of new cylinder.
A solid is in the form of a cylinder with hemispherical ends. Total height of the solid is 19 cm and the diameter of the cylinder is 7 cm. Find the volume and total surface area of the solid.
Two cubes each of volume 27 cm3 are joined end to end to form a solid. Find the surface area of the resulting cuboid.
The boilers are used in thermal power plants to store water and then used to produce steam. One such boiler consists of a cylindrical part in middle and two hemispherical parts at its both ends.
Length of the cylindrical part is 7 m and radius of cylindrical part is `7/2` m.
Find the total surface area and the volume of the boiler. Also, find the ratio of the volume of cylindrical part to the volume of one hemispherical part.

Statement A (Assertion): Total Surface area of the top is the sum of the curved surface area of the hemisphere and the curved surface area of the cone.
Statement R( Reason): Top is obtained by joining the plane surfaces of the hemisphere and cone together.

