Advertisements
Advertisements
प्रश्न
Two cubes each of volume 27 cm3 are joined end to end to form a solid. Find the surface area of the resulting cuboid.
उत्तर
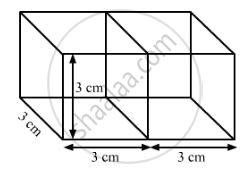
As , volume of a cube = 27 cm3
⇒ (edge)3 = 27
⇒ edge = `root {3}(27)`
⇒ edge = 3 cm
The length of the resulting cuboid , l = 3 + 3 = 6 cm ,
its breath , b = 3 cm and its height , h = 3 cm
Now , the surface area of the resulting cuboid = 2(lb + bh + hl)
= `2 (6 xx 3 + 3 xx 3 + 3 xx 6)`
= 2 (18 + 9 + 18)
= `2 xx 45`
= 90 cm2
APPEARS IN
संबंधित प्रश्न
In Figure 2, ABCD is a trapezium of area 24.5 sq. cm. In it, AD|| BC, ∠ DAB = 900, AD = 10 cm and BC = 4 cm. If ABE is a quadrant of a circle, find the area of the shaded region. [Take π=22/7]
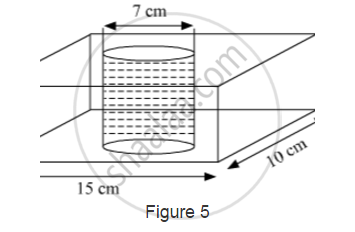
In Fig. 5, from a cuboidal solid metallic block, of dimensions 15cm ✕ 10cm ✕ 5cm, a cylindrical hole of diameter 7 cm is drilled out. Find the surface area of the remaining block [Use
`pi=22/7`]
The diameters of the lower and upper ends of a bucket in the form of a frustum of a cone are 10 cm and 30 cm respectively. If its height is 24 cm, find:
1) The area of the metal sheet used to make the bucket.
2) Why we should avoid the bucket made by ordinary plastic? [Use π = 3.14]
Prove that the surface area of a sphere is equal to the curved surface area of the circumference cylinder__?
A bucket has top and bottom diameter of 40 cm and 20 cm respectively. Find the volume of the bucket if its depth is 12 cm. Also, find the cost of tin sheet used for making the bucket at the rate of Rs. 1.20 per dm2 . (Use π = 3.14)
The perimeters of the ends of a frustum of a right circular cone are 44 cm and 33 cm. If the height of the frustum be 16 cm, find its volume, the slant surface and the total surface.
A metallic cylinder has radius 3 cm and height 5 cm. To reduce its weight, a conical hole is drilled in the cylinder. The conical hole has a radius of `3/2` cm and its depth is `8/9 `cm. Calculate the ratio of the volume of metal left in the cylinder to the volume of metal taken out in conical shape.
In Figure 4, from a rectangular region ABCD with AB = 20 cm, a right triangle AED with AE = 9 cm and DE = 12 cm, is cut off. On the other end, taking BC as diameter, a semicircle is added on outside the region. Find the area of the shaded region.\[[Use\pi = 3 . 14]\]

A solid metal sphere of 6 cm diameter is melted and a circular sheet of thickness 1 cm is prepared. Determine the diameter of the sheet.
If two solid hemispheres of the same base radius r are joined together along their bases, then curved surface area of this new solid is ______.
