Advertisements
Advertisements
Question
Prove that in a right angle triangle, the square of the hypotenuse is equal to the sum of squares of the other two sides.
Solution
“In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.”
Proof: Let ABC be a right triangle where ∠B = 90°.
It has to be proved that AC2 = AB2 + BC2
Construction: Draw BD ⊥ AC
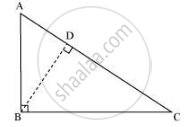
In ΔADB and ΔABC,
∠ADB = ∠ABC [Each is right angle]
∠BAD = ∠BAC [Common angle]
Therefore, by AA similarity criterion, ΔADB ∼ ΔABC
∴ `("AD")/("AB") = ("AB")/("AC")` .....[Sides are proportional in similar triangles]
⇒ AD x AC = AB2 ...(1)
Similarly, it can be proved that ΔBDC ∼ ΔABC
∴ `("CD")/("BC") = ("BC")/("AC")`
⇒ AC x CD = BC2 ...(2)
Adding equations (1) and (2), we obtain
AB2 + BC2 = AD × AC + AC × CD
⇒ AB2 + BC2 = AC (AD + CD)
⇒ AB2 + BC2 = AC × AC
⇒ AB2 + BC2 = AC2
This proves the Pythagoras Theorem.
APPEARS IN
RELATED QUESTIONS
Some question and their alternative answer are given. Select the correct alternative.
If a, b, and c are sides of a triangle and a2 + b2 = c2, name the type of triangle.
In the given figure, AB//CD, AB = 7 cm, BD = 25 cm and CD = 17 cm;
find the length of side BC.
Prove that (1 + cot A - cosec A ) (1 + tan A + sec A) = 2
Show that the triangle ABC is a right-angled triangle; if: AB = 9 cm, BC = 40 cm and AC = 41 cm
The sides of the triangle are given below. Find out which one is the right-angled triangle?
11, 60, 61
PQR is an isosceles triangle with PQ = PR = 10 cm and QR = 12 cm. Find the length of the perpendicular from P to QR.
From the given figure, in ∆ABQ, if AQ = 8 cm, then AB =?

In a quadrilateral ABCD, ∠A + ∠D = 90°. Prove that AC2 + BD2 = AD2 + BC2
[Hint: Produce AB and DC to meet at E.]
In an isosceles triangle PQR, the length of equal sides PQ and PR is 13 cm and base QR is 10 cm. Find the length of perpendicular bisector drawn from vertex P to side QR.
The foot of a ladder is 6 m away from its wall and its top reaches a window 8 m above the ground. If the ladder is shifted in such a way that its foot is 8 m away from the wall, to what height does its top reach?
