Advertisements
Advertisements
प्रश्न
Prove that in a right angle triangle, the square of the hypotenuse is equal to the sum of squares of the other two sides.
उत्तर
“In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.”
Proof: Let ABC be a right triangle where ∠B = 90°.
It has to be proved that AC2 = AB2 + BC2
Construction: Draw BD ⊥ AC
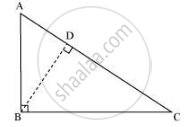
In ΔADB and ΔABC,
∠ADB = ∠ABC [Each is right angle]
∠BAD = ∠BAC [Common angle]
Therefore, by AA similarity criterion, ΔADB ∼ ΔABC
∴ `("AD")/("AB") = ("AB")/("AC")` .....[Sides are proportional in similar triangles]
⇒ AD x AC = AB2 ...(1)
Similarly, it can be proved that ΔBDC ∼ ΔABC
∴ `("CD")/("BC") = ("BC")/("AC")`
⇒ AC x CD = BC2 ...(2)
Adding equations (1) and (2), we obtain
AB2 + BC2 = AD × AC + AC × CD
⇒ AB2 + BC2 = AC (AD + CD)
⇒ AB2 + BC2 = AC × AC
⇒ AB2 + BC2 = AC2
This proves the Pythagoras Theorem.
APPEARS IN
संबंधित प्रश्न
ABC is a right-angled triangle, right-angled at A. A circle is inscribed in it. The lengths of the two sides containing the right angle are 5 cm and 12 cm. Find the radius of the circle
Walls of two buildings on either side of a street are parallel to each other. A ladder 5.8 m long is placed on the street such that its top just reaches the window of a building at the height of 4 m. On turning the ladder over to the other side of the street, its top touches the window of the other building at a height 4.2 m. Find the width of the street.
In the following figure, AD is perpendicular to BC and D divides BC in the ratio 1: 3.
Prove that : 2AC2 = 2AB2 + BC2
In triangle ABC, ∠B = 90o and D is the mid-point of BC.
Prove that: AC2 = AD2 + 3CD2.
Choose the correct alternative:
In right-angled triangle PQR, if hypotenuse PR = 12 and PQ = 6, then what is the measure of ∠P?
In Fig. 3, ∠ACB = 90° and CD ⊥ AB, prove that CD2 = BD x AD.

Find the Pythagorean triplet from among the following set of numbers.
2, 6, 7
In a right-angled triangle PQR, right-angled at Q, S and T are points on PQ and QR respectively such as PT = SR = 13 cm, QT = 5 cm and PS = TR. Find the length of PQ and PS.
Prove that the area of the semicircle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the semicircles drawn on the other two sides of the triangle.
Two circles having same circumference are congruent.
