Advertisements
Advertisements
प्रश्न
Prove that in a right angle triangle, the square of the hypotenuse is equal to the sum of squares of the other two sides.
उत्तर
“In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.”
Proof: Let ABC be a right triangle where ∠B = 90°.
It has to be proved that AC2 = AB2 + BC2
Construction: Draw BD ⊥ AC
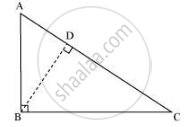
In ΔADB and ΔABC,
∠ADB = ∠ABC [Each is right angle]
∠BAD = ∠BAC [Common angle]
Therefore, by AA similarity criterion, ΔADB ∼ ΔABC
∴ `("AD")/("AB") = ("AB")/("AC")` .....[Sides are proportional in similar triangles]
⇒ AD x AC = AB2 ...(1)
Similarly, it can be proved that ΔBDC ∼ ΔABC
∴ `("CD")/("BC") = ("BC")/("AC")`
⇒ AC x CD = BC2 ...(2)
Adding equations (1) and (2), we obtain
AB2 + BC2 = AD × AC + AC × CD
⇒ AB2 + BC2 = AC (AD + CD)
⇒ AB2 + BC2 = AC × AC
⇒ AB2 + BC2 = AC2
This proves the Pythagoras Theorem.
APPEARS IN
संबंधित प्रश्न
ABCD is a rhombus. Prove that AB2 + BC2 + CD2 + DA2= AC2 + BD2
Sides of triangle are given below. Determine it is a right triangle or not? In case of a right triangle, write the length of its hypotenuse. 13 cm, 12 cm, 5 cm
Tick the correct answer and justify: In ΔABC, AB = `6sqrt3` cm, AC = 12 cm and BC = 6 cm.
The angle B is:
In the given figure, ABC is a triangle in which ∠ABC> 90° and AD ⊥ CB produced. Prove that AC2 = AB2 + BC2 + 2BC.BD.

Which of the following can be the sides of a right triangle?
2.5 cm, 6.5 cm, 6 cm
In the case of right-angled triangles, identify the right angles.
Pranali and Prasad started walking to the East and to the North respectively, from the same point and at the same speed. After 2 hours distance between them was \[15\sqrt{2}\]
km. Find their speed per hour.
In the figure: ∠PSQ = 90o, PQ = 10 cm, QS = 6 cm and RQ = 9 cm. Calculate the length of PR.
In figure AB = BC and AD is perpendicular to CD.
Prove that: AC2 = 2BC. DC.
Choose the correct alternative:
If length of sides of a triangle are a, b, c and a2 + b2 = c2, then which type of triangle it is?
If two legs of a right triangle are equal to two legs of another right triangle, then the right triangles are congruent.
