Advertisements
Advertisements
Question
PQR is an isosceles triangle with PQ = PR = 10 cm and QR = 12 cm. Find the length of the perpendicular from P to QR.
Solution
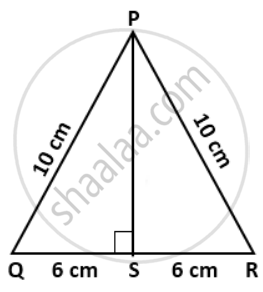
Since, PQR is an isosceles triangle and PS ⊥ QR,
therefore it divides QR into two equal parts.
In ΔPSQ, ∠S = 90°
∴ PQ2 = PS2 + QS2 ....(By Pythagoras Theorem)
⇒ PS2 = PQ2 - QS2
= 102 - 62
= 100 - 36
= 64
⇒ PS = 8cm.
APPEARS IN
RELATED QUESTIONS
The perpendicular AD on the base BC of a ∆ABC intersects BC at D so that DB = 3 CD. Prove that `2"AB"^2 = 2"AC"^2 + "BC"^2`
A guy wire attached to a vertical pole of height 18 m is 24 m long and has a stake attached to the other end. How far from the base of the pole should the stake be driven so that the wire will be taut?
In an equilateral triangle, prove that three times the square of one side is equal to four times the square of one of its altitudes.
In the given figure, AD is a median of a triangle ABC and AM ⊥ BC. Prove that:

`"AC"^2 = "AD"^2 + "BC"."DM" + (("BC")/2)^2`
Identify, with reason, if the following is a Pythagorean triplet.
(11, 60, 61)
Some question and their alternative answer are given. Select the correct alternative.
If a, b, and c are sides of a triangle and a2 + b2 = c2, name the type of triangle.
In ΔABC, Find the sides of the triangle, if:
- AB = ( x - 3 ) cm, BC = ( x + 4 ) cm and AC = ( x + 6 ) cm
- AB = x cm, BC = ( 4x + 4 ) cm and AC = ( 4x + 5) cm
In the given figure, ∠B = 90°, XY || BC, AB = 12 cm, AY = 8cm and AX : XB = 1 : 2 = AY : YC.
Find the lengths of AC and BC.

In a rectangle ABCD,
prove that: AC2 + BD2 = AB2 + BC2 + CD2 + DA2.
Choose the correct alternative:
In right-angled triangle PQR, if hypotenuse PR = 12 and PQ = 6, then what is the measure of ∠P?
Find the value of (sin2 33 + sin2 57°)
In the given figure, BL and CM are medians of a ∆ABC right-angled at A. Prove that 4 (BL2 + CM2) = 5 BC2.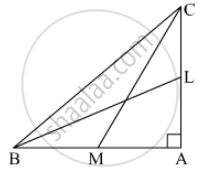
Find the length of the perpendicular of a triangle whose base is 5cm and the hypotenuse is 13cm. Also, find its area.
A ladder 15m long reaches a window which is 9m above the ground on one side of a street. Keeping its foot at the same point, the ladder is turned to other side of the street to reach a window 12m high. Find the width of the street.
From a point O in the interior of aΔABC, perpendicular OD, OE and OF are drawn to the sides BC, CA and AB respectively. Prove that: AF2 + BD2 + CE2 = OA2 + OB2 + OC2 - OD2 - OE2 - OF2
For going to a city B from city A, there is a route via city C such that AC ⊥ CB, AC = 2x km and CB = 2(x + 7) km. It is proposed to construct a 26 km highway which directly connects the two cities A and B. Find how much distance will be saved in reaching city B from city A after the construction of the highway.
If S is a point on side PQ of a ΔPQR such that PS = QS = RS, then ______.
In ∆PQR, PD ⊥ QR such that D lies on QR. If PQ = a, PR = b, QD = c and DR = d, prove that (a + b)(a – b) = (c + d)(c – d).
In the adjoining figure, a tangent is drawn to a circle of radius 4 cm and centre C, at the point S. Find the length of the tangent ST, if CT = 10 cm.

Two squares are congruent, if they have same ______.
