Advertisements
Advertisements
Question
Show that the triangle ABC is a right-angled triangle; if: AB = 9 cm, BC = 40 cm and AC = 41 cm
Solution
AB = 9 cm
CB = 40 cm
AC = 41 cm
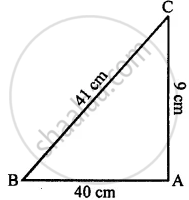
The given triangle will be a right-angled triangle if square of its largest side is equal to the sum of the squares on the other two sides.
According to Pythagoras Theorem,
(AC)2 = (BC)2 + (AB)2
(41)2 = (40)2 + (9)2
1681 = 1600 + 81
1681 = 1681
Hence, it is a right-angled triangle ABC.
APPEARS IN
RELATED QUESTIONS
Side of a triangle is given, determine it is a right triangle.
`(2a – 1) cm, 2\sqrt { 2a } cm, and (2a + 1) cm`
ABC is an isosceles triangle right angled at C. Prove that AB2 = 2AC2
A ladder 10 m long reaches a window 8 m above the ground. Find the distance of the foot of the ladder from base of the wall.
In the given figure, point T is in the interior of rectangle PQRS, Prove that, TS2 + TQ2 = TP2 + TR2 (As shown in the figure, draw seg AB || side SR and A-T-B)

Find the length of the hypotenuse of a right angled triangle if remaining sides are 9 cm and 12 cm.
Digonals of parallelogram WXYZ intersect at point O. If OY =5, find WY.
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AB2 + AC2 = 2AD2 + `(1)/(2)"BC"^2`
There are two paths that one can choose to go from Sarah’s house to James's house. One way is to take C street, and the other way requires to take B street and then A street. How much shorter is the direct path along C street?

If the areas of two circles are the same, they are congruent.
Two poles of 10 m and 15 m stand upright on a plane ground. If the distance between the tops is 13 m, find the distance between their feet.
