Advertisements
Advertisements
प्रश्न
Show that the triangle ABC is a right-angled triangle; if: AB = 9 cm, BC = 40 cm and AC = 41 cm
उत्तर
AB = 9 cm
CB = 40 cm
AC = 41 cm
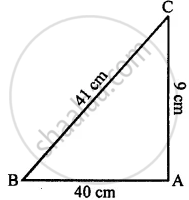
The given triangle will be a right-angled triangle if square of its largest side is equal to the sum of the squares on the other two sides.
According to Pythagoras Theorem,
(AC)2 = (BC)2 + (AB)2
(41)2 = (40)2 + (9)2
1681 = 1600 + 81
1681 = 1681
Hence, it is a right-angled triangle ABC.
APPEARS IN
संबंधित प्रश्न
In an equilateral triangle, prove that three times the square of one side is equal to four times the square of one of its altitudes.
Which of the following can be the sides of a right triangle?
2 cm, 2 cm, 5 cm
In the case of right-angled triangles, identify the right angles.
In the given figure, M is the midpoint of QR. ∠PRQ = 90°. Prove that, PQ2 = 4PM2 – 3PR2.

Prove that `(sin θ + cosec θ)^2 + (cos θ + sec θ)^2 = 7 + tan^2 θ + cot^2 θ`.
In the given figure, AD = 13 cm, BC = 12 cm, AB = 3 cm and angle ACD = angle ABC = 90°. Find the length of DC.

Use the information given in the figure to find the length AD.

The sides of the triangle are given below. Find out which one is the right-angled triangle?
1.5, 1.6, 1.7
The length of the diagonals of rhombus are 24cm and 10cm. Find each side of the rhombus.
If ΔABC ~ ΔPQR, `("ar" triangle "ABC")/("ar" triangle "PQR") = 9/4` and AB = 18 cm, then the length of PQ is ______.
Sides AB and BE of a right triangle, right-angled at B are of lengths 16 cm and 8 cm respectively. The length of the side of largest square FDGB that can be inscribed in the triangle ABE is ______.

