Advertisements
Advertisements
प्रश्न
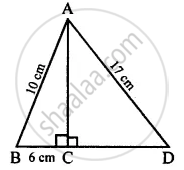
In the given figure, angle ACB = 90° = angle ACD. If AB = 10 m, BC = 6 cm and AD = 17 cm, find :
(i) AC
(ii) CD

उत्तर
∆ ABD
∠ACB = ∠ACD = 90°
and AB = 10 cm, BC = 6 cm and AD = 17 cm
To find:
(i) Length of AC
(ii) Length of CD
Proof:
(i) In right-angled triangle ABC
BC = 6 cm, AB = 110 cm
According to Pythagoras Theorem,
AB2 = AC2 + BC2
(10)2 = (AC)2 + (6)2
100 = (AC)2 + 36
AC2 = 100 − 36 = 64 cm
AC2 = 64 cm
∴ AC = `sqrt(8xx8)` = 8 cm
(ii) In right-angle triangle ACD
AD = 17 cm, AC = 8 cm
According to Pythagoras Theorem,
(AD)2 = (AC)2 + (CD)2
(17)2 = (8)2 + (CD)2
289 – 64 = CD2
225 = CD2
CD =`sqrt(15xx15)` = 15 cm
APPEARS IN
संबंधित प्रश्न
The perpendicular AD on the base BC of a ∆ABC intersects BC at D so that DB = 3 CD. Prove that `2"AB"^2 = 2"AC"^2 + "BC"^2`
Find the perimeter of the rectangle whose length is 40 cm and a diagonal is 41 cm.
In the given figure, ∆ABC is an equilateral triangle of side 3 units. Find the coordinates of the other two vertices ?

In triangle ABC, AB = AC = x, BC = 10 cm and the area of the triangle is 60 cm2.
Find x.
A ladder 15m long reaches a window which is 9m above the ground on one side of a street. Keeping its foot at the same point, the ladder is turned to other side of the street to reach a window 12m high. Find the width of the street.
From a point O in the interior of aΔABC, perpendicular OD, OE and OF are drawn to the sides BC, CA and AB respectively. Prove that: AF2 + BD2 + CE2 = OA2 + OB2 + OC2 - OD2 - OE2 - OF2
In a square PQRS of side 5 cm, A, B, C and D are points on sides PQ, QR, RS and SP respectively such as PA = PD = RB = RC = 2 cm. Prove that ABCD is a rectangle. Also, find the area and perimeter of the rectangle.
In a right angled triangle, if length of hypotenuse is 25 cm and height is 7 cm, then what is the length of its base?
Two squares having same perimeter are congruent.
If the hypotenuse of one right triangle is equal to the hypotenuse of another right triangle, then the triangles are congruent.
