Advertisements
Advertisements
प्रश्न
In a square PQRS of side 5 cm, A, B, C and D are points on sides PQ, QR, RS and SP respectively such as PA = PD = RB = RC = 2 cm. Prove that ABCD is a rectangle. Also, find the area and perimeter of the rectangle.
उत्तर
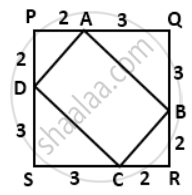
In ΔAPD, ∠P = 90°
∴ AD2 = AP2 + PD2
= 22 + 22
= 4 + 4
= 8
⇒ AD = `2sqrt(2)"cm"`
Similarly, we can prove that in ΔBRC,
BC = `2sqrt(2)"cm"`
∴ AD = BC ....(i)
In ΔAQB, ∠Q = 90°
∴ AB2 = AQ2 + BQ2
= 32 + 32
= 9 + 9
= 18
⇒ AB = `3sqrt(2)"cm"`
Similarly, we can prove that in ΔCSD,
CD = `3sqrt(2)"cm"`
∴ AB = CD ....(ii)
|Again, in ΔAPD,
AP = PD
⇒ ∠PAD = ∠PDA = 45°
Also, in ΔAQB,
AQ = BQ
⇒ ∠QAB = ∠QBA = 45°
Now, ∠PAD + ∠DAB + ∠QAB = 180°
⇒ 45° + ∠DAB + 45° = 180°
⇒ ∠DAB = 90°
Similarly, we can prove that ∠ABC, ∠BCD and ∠ADC are 90° each.
Thus, ABCD is a rectangle as opposite as opposite sides are equal and each angle is 90°.
Now,
Area of a rectangle ABCD
= AD x AB
= `2sqrt(2) xx 3sqrt(2)`
= 12cm2
Perimeter of a rectangle ABCD
= AB + BC + CD + AD
= `2sqrt(2) + 3sqrt(2) + 2sqrt(2) + 3sqrt(2)`
= `10sqrt(2)"cm"`.
APPEARS IN
संबंधित प्रश्न
In figure, ∠B of ∆ABC is an acute angle and AD ⊥ BC, prove that AC2 = AB2 + BC2 – 2BC × BD
ABCD is a rhombus. Prove that AB2 + BC2 + CD2 + DA2= AC2 + BD2
Sides of triangle are given below. Determine it is a right triangle or not? In case of a right triangle, write the length of its hypotenuse. 50 cm, 80 cm, 100 cm
Which of the following can be the sides of a right triangle?
2.5 cm, 6.5 cm, 6 cm
In the case of right-angled triangles, identify the right angles.
In the given figure, ∠DFE = 90°, FG ⊥ ED, If GD = 8, FG = 12, find (1) EG (2) FD and (3) EF

In ∆ABC, AB = 10, AC = 7, BC = 9, then find the length of the median drawn from point C to side AB.
A man goes 40 m due north and then 50 m due west. Find his distance from the starting point.
In the figure, given below, AD ⊥ BC.
Prove that: c2 = a2 + b2 - 2ax.
In the following figure, OP, OQ, and OR are drawn perpendiculars to the sides BC, CA and AB respectively of triangle ABC.
Prove that: AR2 + BP2 + CQ2 = AQ2 + CP2 + BR2

If the angles of a triangle are 30°, 60°, and 90°, then shown that the side opposite to 30° is half of the hypotenuse, and the side opposite to 60° is `sqrt(3)/2` times of the hypotenuse.
If P and Q are the points on side CA and CB respectively of ΔABC, right angled at C, prove that (AQ2 + BP2 ) = (AB2 + PQ2)
In the given figure, angle BAC = 90°, AC = 400 m, and AB = 300 m. Find the length of BC.

The length of the diagonals of rhombus are 24cm and 10cm. Find each side of the rhombus.
In the given figure. PQ = PS, P =R = 90°. RS = 20 cm and QR = 21 cm. Find the length of PQ correct to two decimal places.
In a right angled triangle, the hypotenuse is the greatest side
A 5 m long ladder is placed leaning towards a vertical wall such that it reaches the wall at a point 4 m high. If the foot of the ladder is moved 1.6 m towards the wall, then find the distance by which the top of the ladder would slide upwards on the wall.
If S is a point on side PQ of a ΔPQR such that PS = QS = RS, then ______.
The longest side of a right angled triangle is called its ______.
In a triangle, sum of squares of two sides is equal to the square of the third side.
