Advertisements
Advertisements
प्रश्न
If S is a point on side PQ of a ΔPQR such that PS = QS = RS, then ______.
पर्याय
PR . QR = RS2
QS2 + RS2 = QR2
PR2 + QR2 = PQ2
PS2 + RS2 = PR2
उत्तर
If S is a point on side PQ of a ΔPQR such that PS = QS = RS, then PR2 + QR2 = PQ2.
Explanation:
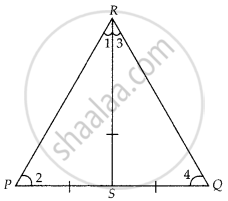
Given, in ∆PQR,
PS = QS = RS ...(i)
In ∆PSR,
PS = RS ...[From equation (i)]
⇒ ∠1 = ∠2 ...(ii) [Angles opposite to equal sides are equal]
Similarly, in ∆RSQ,
RS = SQ
⇒ ∠3 = ∠4 ...(iii) [Angles opposite to equal sides are equal]
Now, in ∆PQR,
Sum of angles = 180°
⇒ ∠P + ∠Q + ∠P = 180°
⇒ ∠2 + ∠4 + ∠1 + ∠3 = 180°
⇒ ∠1 + ∠3 + ∠1 + ∠3 = 180°
⇒ 2(∠1 + ∠3) = 180°
⇒ ∠1 + ∠3 = `180^circ/2` = 90°
∴ ∠R = 90°
In ∆PQR, by Pythagoras theorem,
PR2 + QR2 = PQ2
APPEARS IN
संबंधित प्रश्न
An aeroplane leaves an airport and flies due north at a speed of 1,000 km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1,200 km per hour. How far apart will be the two planes after `1 1/2` hours?
The perimeter of a triangle with vertices (0, 4), (0, 0) and (3, 0) is
(A)\[7 + \sqrt{5}\]
(B) 5
(C) 10
(D) 12
In triangle ABC, given below, AB = 8 cm, BC = 6 cm and AC = 3 cm. Calculate the length of OC.

In triangle ABC, angle A = 90o, CA = AB and D is the point on AB produced.
Prove that DC2 - BD2 = 2AB.AD.
In the given figure, BL and CM are medians of a ∆ABC right-angled at A. Prove that 4 (BL2 + CM2) = 5 BC2.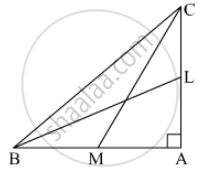
Find the Pythagorean triplet from among the following set of numbers.
9, 40, 41
The sides of the triangle are given below. Find out which one is the right-angled triangle?
11, 12, 15
Each side of rhombus is 10cm. If one of its diagonals is 16cm, find the length of the other diagonals.
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AB2 + AC2 = 2AD2 + `(1)/(2)"BC"^2`
If the areas of two circles are the same, they are congruent.
