Advertisements
Advertisements
प्रश्न
A man goes 40 m due north and then 50 m due west. Find his distance from the starting point.
उत्तर
Here, we need to measure the distance AB as shown in the figure below,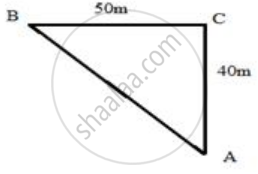
Pythagoras theorem states that in a right-angled triangle, the square on the hypotenuse is equal to the sum of the squares on the remaining two sides.
Therefore, in this case
AB2 = BC2 + CA2
AB2 = 502 + 402
AB2 = 2500 + 1600
AB2 = 4100
AB = 64.03
Therefore the required distance is 64.03 m.
APPEARS IN
संबंधित प्रश्न
An aeroplane leaves an airport and flies due north at a speed of 1,000 km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1,200 km per hour. How far apart will be the two planes after `1 1/2` hours?
Two poles of heights 6 m and 11 m stand on a plane ground. If the distance between the feet of the poles is 12 m, find the distance between their tops.
Which of the following can be the sides of a right triangle?
2.5 cm, 6.5 cm, 6 cm
In the case of right-angled triangles, identify the right angles.
Find the perimeter of the rectangle whose length is 40 cm and a diagonal is 41 cm.
The diagonals of a rhombus measure 16 cm and 30 cm. Find its perimeter.
Identify, with reason, if the following is a Pythagorean triplet.
(5, 12, 13)
In an isosceles triangle, length of the congruent sides is 13 cm and its base is 10 cm. Find the distance between the vertex opposite the base and the centroid.
In a trapezium ABCD, seg AB || seg DC seg BD ⊥ seg AD, seg AC ⊥ seg BC, If AD = 15, BC = 15 and AB = 25. Find A(▢ABCD)

The given figure shows a quadrilateral ABCD in which AD = 13 cm, DC = 12 cm, BC = 3 cm and ∠ABD = ∠BCD = 90o. Calculate the length of AB.
In triangle ABC, given below, AB = 8 cm, BC = 6 cm and AC = 3 cm. Calculate the length of OC.

In the figure, given below, AD ⊥ BC.
Prove that: c2 = a2 + b2 - 2ax.
Find the length of diagonal of the square whose side is 8 cm.
In Fig. 3, ∠ACB = 90° and CD ⊥ AB, prove that CD2 = BD x AD.

In triangle PQR, angle Q = 90°, find: PR, if PQ = 8 cm and QR = 6 cm
The perimeters of two similar triangles ABC and PQR are 60 cm and 36 cm respectively. If PQ = 9 cm, then AB equals ______.
In the adjoining figure, a tangent is drawn to a circle of radius 4 cm and centre C, at the point S. Find the length of the tangent ST, if CT = 10 cm.

The longest side of a right angled triangle is called its ______.
Two rectangles are congruent, if they have same ______ and ______.
The hypotenuse (in cm) of a right angled triangle is 6 cm more than twice the length of the shortest side. If the length of third side is 6 cm less than thrice the length of shortest side, then find the dimensions of the triangle.
