Advertisements
Advertisements
प्रश्न
A ladder 13 m long rests against a vertical wall. If the foot of the ladder is 5 m from the foot of the wall, find the distance of the other end of the ladder from the ground.
उत्तर
The pictorial representation of the given problem is given below,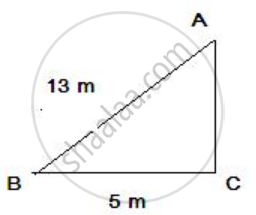
Pythagoras theorem states that in a right-angled triangle, the square on the hypotenuse is equal to the sum of the squares on the remaining two sides.
Here, AB is the hypotenuse.
Therefore applying the Pythagoras theorem we get,
AB2 = BC2 + CA2
132 = 52 + CA2
CA2 = 132 - 52
CA2 = 144
CA = 12 m
Therefore, the distance of the other end of the ladder from the ground is 12m.
APPEARS IN
संबंधित प्रश्न
In a right triangle ABC, right-angled at B, BC = 12 cm and AB = 5 cm. The radius of the circle inscribed in the triangle (in cm) is
(A) 4
(B) 3
(C) 2
(D) 1
A man goes 10 m due east and then 24 m due north. Find the distance from the starting point
From a point O in the interior of a ∆ABC, perpendicular OD, OE and OF are drawn to the sides BC, CA and AB respectively. Prove
that :
`(i) AF^2 + BD^2 + CE^2 = OA^2 + OB^2 + OC^2 – OD^2 – OE^2 – OF^2`
`(ii) AF^2 + BD^2 + CE^2 = AE^2 + CD^2 + BF^2`
The perpendicular AD on the base BC of a ∆ABC intersects BC at D so that DB = 3 CD. Prove that `2"AB"^2 = 2"AC"^2 + "BC"^2`
In Figure, ABD is a triangle right angled at A and AC ⊥ BD. Show that AB2 = BC × BD

A 15 m long ladder reached a window 12 m high from the ground on placing it against a wall at a distance a. Find the distance of the foot of the ladder from the wall.

Find the perimeter of the rectangle whose length is 40 cm and a diagonal is 41 cm.
Identify, with reason, if the following is a Pythagorean triplet.
(24, 70, 74)
Find the side and perimeter of a square whose diagonal is 10 cm.
In ∆ABC, AB = 10, AC = 7, BC = 9, then find the length of the median drawn from point C to side AB.
In equilateral Δ ABC, AD ⊥ BC and BC = x cm. Find, in terms of x, the length of AD.
In the following Figure ∠ACB= 90° and CD ⊥ AB, prove that CD2 = BD × AD

Triangle ABC is right-angled at vertex A. Calculate the length of BC, if AB = 18 cm and AC = 24 cm.
The sides of a certain triangle is given below. Find, which of them is right-triangle
16 cm, 20 cm, and 12 cm
In ΔABC, AD is perpendicular to BC. Prove that: AB2 + CD2 = AC2 + BD2
From a point O in the interior of aΔABC, perpendicular OD, OE and OF are drawn to the sides BC, CA and AB respectively. Prove that: AF2 + BD2 + CE2 = OA2 + OB2 + OC2 - OD2 - OE2 - OF2
∆ABC is right-angled at C. If AC = 5 cm and BC = 12 cm. find the length of AB.
Choose the correct alternative:
If length of sides of a triangle are a, b, c and a2 + b2 = c2, then which type of triangle it is?
A 5 m long ladder is placed leaning towards a vertical wall such that it reaches the wall at a point 4 m high. If the foot of the ladder is moved 1.6 m towards the wall, then find the distance by which the top of the ladder would slide upwards on the wall.
If the areas of two circles are the same, they are congruent.
