Advertisements
Advertisements
प्रश्न
The diagonals of a rhombus measure 16 cm and 30 cm. Find its perimeter.
उत्तर
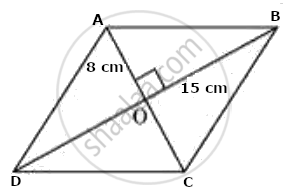
Let ABCD be a rhombus (all sides are of equal length) and its diagonals, AC and BD, are intersecting each other at point O. Diagonals in a rhombus bisect each other at 90°. It can be observed that
AO = `(AC)/2`
= `16/2`
= 8 cm
BO = `(BD)/2`
= `30/2`
= 15 cm
By applying Pythagoras theorem in ΔAOB,
OA2 + OB2 = AB2
82 + 152 = AB2
64 + 225 = AB2
289 = AB2
AB = 17
Therefore, the length of the side of rhombus is 17 cm.
Perimeter of rhombus = 4 × Side of the rhombus
= 4 × 17
= 68 cm
APPEARS IN
संबंधित प्रश्न
Identify, with reason, if the following is a Pythagorean triplet.
(3, 5, 4)
In ΔABC, Find the sides of the triangle, if:
- AB = ( x - 3 ) cm, BC = ( x + 4 ) cm and AC = ( x + 6 ) cm
- AB = x cm, BC = ( 4x + 4 ) cm and AC = ( 4x + 5) cm
In triangle ABC, AB = AC = x, BC = 10 cm and the area of the triangle is 60 cm2.
Find x.
In figure AB = BC and AD is perpendicular to CD.
Prove that: AC2 = 2BC. DC.
Triangle PQR is right-angled at vertex R. Calculate the length of PR, if: PQ = 34 cm and QR = 33.6 cm.
In the given figure, angle ACB = 90° = angle ACD. If AB = 10 m, BC = 6 cm and AD = 17 cm, find :
(i) AC
(ii) CD

The sides of the triangle are given below. Find out which one is the right-angled triangle?
11, 60, 61
Two trains leave a railway station at the same time. The first train travels due west and the second train due north. The first train travels at a speed of `(20 "km")/"hr"` and the second train travels at `(30 "km")/"hr"`. After 2 hours, what is the distance between them?
The hypotenuse of a right angled triangle of sides 12 cm and 16 cm is __________
The longest side of a right angled triangle is called its ______.
