Advertisements
Advertisements
प्रश्न
Triangle PQR is right-angled at vertex R. Calculate the length of PR, if: PQ = 34 cm and QR = 33.6 cm.
उत्तर
Given: ∆PQR right angled at R and PQ = 34 cm, QR = 33.6 cm.
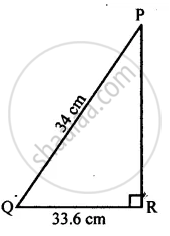
To find: Length of PR.
According to Pythagoras' Theorem,
PR2 + QR2 = PQ2
PR2 + 33.62 = 342
PR2+ 1128.96= 1156
PR2 = 1156 − 1128.96
PR = `sqrt27.04`
∴ PR = 5.2 cm
APPEARS IN
संबंधित प्रश्न
Two towers of heights 10 m and 30 m stand on a plane ground. If the distance between their feet is 15 m, find the distance between their tops
ABCD is a rhombus. Prove that AB2 + BC2 + CD2 + DA2= AC2 + BD2
ABC is an isosceles triangle with AC = BC. If AB2 = 2AC2, prove that ABC is a right triangle.
A ladder 10 m long reaches a window 8 m above the ground. Find the distance of the foot of the ladder from base of the wall.
A ladder 13 m long rests against a vertical wall. If the foot of the ladder is 5 m from the foot of the wall, find the distance of the other end of the ladder from the ground.
In the given figure, angle ACB = 90° = angle ACD. If AB = 10 m, BC = 6 cm and AD = 17 cm, find :
(i) AC
(ii) CD

Find the Pythagorean triplet from among the following set of numbers.
4, 7, 8
The sides of the triangle are given below. Find out which one is the right-angled triangle?
11, 12, 15
The sides of the triangle are given below. Find out which one is the right-angled triangle?
1.5, 1.6, 1.7
In an isosceles triangle PQR, the length of equal sides PQ and PR is 13 cm and base QR is 10 cm. Find the length of perpendicular bisector drawn from vertex P to side QR.
