Advertisements
Advertisements
Question
Triangle PQR is right-angled at vertex R. Calculate the length of PR, if: PQ = 34 cm and QR = 33.6 cm.
Solution
Given: ∆PQR right angled at R and PQ = 34 cm, QR = 33.6 cm.
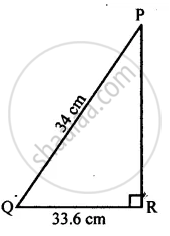
To find: Length of PR.
According to Pythagoras' Theorem,
PR2 + QR2 = PQ2
PR2 + 33.62 = 342
PR2+ 1128.96= 1156
PR2 = 1156 − 1128.96
PR = `sqrt27.04`
∴ PR = 5.2 cm
APPEARS IN
RELATED QUESTIONS
In Figure, ABD is a triangle right angled at A and AC ⊥ BD. Show that AB2 = BC × BD

Prove that the sum of the squares of the sides of a rhombus is equal to the sum of the squares of its diagonals
A tree is broken at a height of 5 m from the ground and its top touches the ground at a distance of 12 m from the base of the tree. Find the original height of the tree.
Identify, with reason, if the following is a Pythagorean triplet.
(5, 12, 13)
In the following figure, OP, OQ, and OR are drawn perpendiculars to the sides BC, CA and AB respectively of triangle ABC.
Prove that: AR2 + BP2 + CQ2 = AQ2 + CP2 + BR2

In a rectangle ABCD,
prove that: AC2 + BD2 = AB2 + BC2 + CD2 + DA2.
In triangle ABC, ∠B = 90o and D is the mid-point of BC.
Prove that: AC2 = AD2 + 3CD2.
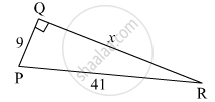
In the figure below, find the value of 'x'.
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AB2 + AC2 = 2AD2 + `(1)/(2)"BC"^2`
A point OI in the interior of a rectangle ABCD is joined with each of the vertices A, B, C and D. Prove that OB2 + OD2 = OC2 + OA2
