Advertisements
Advertisements
Question
A point OI in the interior of a rectangle ABCD is joined with each of the vertices A, B, C and D. Prove that OB2 + OD2 = OC2 + OA2
Solution
Let ABCD be the given rectangle and let O be a point within it.
Join OA, OB, OC and OD.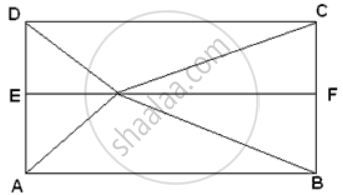
Through O, draw EOF || AB. Then, ABFE is a rectangle.
In right triangles ΔOEA and ΔOFC, we have
OA2 = OE2 + AE2 and OC2 = OF2 + CF2
⇒ OA2 + OC2 = (OE2 + AE2) + (OF2 + CF2)
⇒ OA2 + OC2 = OE2 + OF2 + AE2 + CF2 ......(i)
Now, in right triangles OFB and ODE, we have
OB2 = OF2 + FB2 and OD2 = OE2 + DE2
⇒ OB2 + OD2 = (OF2 + FB2) + (OE2 + DE2)
⇒ OB2 + OD2 = OE2 + OF2 + DE2 + BF2
⇒ OB2 + OD2 = OE2 + OF2 + CF2 + AE2 [∵ DE = CF and AE = BF]....(ii)
From (i) and (ii), we get
OA2 + OC2 = OB2 + OD2.
APPEARS IN
RELATED QUESTIONS
Sides of triangle are given below. Determine it is a right triangle or not? In case of a right triangle, write the length of its hypotenuse. 50 cm, 80 cm, 100 cm
In the given figure, ABC is a triangle in which ∠ABC < 90° and AD ⊥ BC. Prove that AC2 = AB2 + BC2 − 2BC.BD.

Which of the following can be the sides of a right triangle?
2 cm, 2 cm, 5 cm
In the case of right-angled triangles, identify the right angles.
In ∆ABC, ∠BAC = 90°, seg BL and seg CM are medians of ∆ABC. Then prove that:
4(BL2 + CM2) = 5 BC2

In the figure: ∠PSQ = 90o, PQ = 10 cm, QS = 6 cm and RQ = 9 cm. Calculate the length of PR.
In triangle ABC, AB = AC = x, BC = 10 cm and the area of the triangle is 60 cm2.
Find x.
In triangle ABC, AB = AC and BD is perpendicular to AC.
Prove that: BD2 - CD2 = 2CD × AD
Choose the correct alternative:
In right-angled triangle PQR, if hypotenuse PR = 12 and PQ = 6, then what is the measure of ∠P?
Triangle PQR is right-angled at vertex R. Calculate the length of PR, if: PQ = 34 cm and QR = 33.6 cm.
In the given figure, AD = 13 cm, BC = 12 cm, AB = 3 cm and angle ACD = angle ABC = 90°. Find the length of DC.

In the figure below, find the value of 'x'.

In ΔABC, AD is perpendicular to BC. Prove that: AB2 + CD2 = AC2 + BD2
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AB2 = AD2 - BC x CE + `(1)/(4)"BC"^2`
In a right-angled triangle PQR, right-angled at Q, S and T are points on PQ and QR respectively such as PT = SR = 13 cm, QT = 5 cm and PS = TR. Find the length of PQ and PS.
Determine whether the triangle whose lengths of sides are 3 cm, 4 cm, 5 cm is a right-angled triangle.
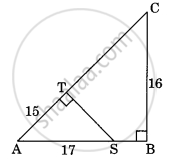
In the given figure, ∠T and ∠B are right angles. If the length of AT, BC and AS (in centimeters) are 15, 16, and 17 respectively, then the length of TC (in centimeters) is ______.
Two squares are congruent, if they have same ______.
In a triangle, sum of squares of two sides is equal to the square of the third side.
The hypotenuse (in cm) of a right angled triangle is 6 cm more than twice the length of the shortest side. If the length of third side is 6 cm less than thrice the length of shortest side, then find the dimensions of the triangle.
Height of a pole is 8 m. Find the length of rope tied with its top from a point on the ground at a distance of 6 m from its bottom.
