Advertisements
Advertisements
Question
The hypotenuse (in cm) of a right angled triangle is 6 cm more than twice the length of the shortest side. If the length of third side is 6 cm less than thrice the length of shortest side, then find the dimensions of the triangle.
Solution
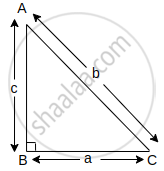
Let ΔABC be the right angle triangle, right angled at B, as shown in the figure.
Also, let AB = c cm, BC = a cm and AC = b cm
Then, according to the given information, we have
b = 6 + 2a .....(i) (Let a be the shortest side)
and c = 3a – 6 ...(ii)
We know that, b2 = c2 + a2
⇒ (6 + 2a)2 = (3a – 6)2 + a2 ...[Using (i) and (ii)]
⇒ 36 + 4a2 + 24a = 9a2 + 36 – 36a + a2
⇒ 60a = 6a2
⇒ 6a = 60 ...[∵ a cannot be zero]
⇒ a = 10 cm
Now, from equation (i),
b = 6 + 2 × 10 = 26
and from equation (ii),
c = 3 × 10 – 6 = 24
Thus, the dimensions of the triangle are 10 cm, 24 cm and 26 cm.
RELATED QUESTIONS
Two towers of heights 10 m and 30 m stand on a plane ground. If the distance between their feet is 15 m, find the distance between their tops
Sides of triangle are given below. Determine it is a right triangle or not? In case of a right triangle, write the length of its hypotenuse. 7 cm, 24 cm, 25 cm
ABC is an equilateral triangle of side 2a. Find each of its altitudes.
Find the length of the hypotenuse of a right angled triangle if remaining sides are 9 cm and 12 cm.
In triangle ABC, AB = AC and BD is perpendicular to AC.
Prove that: BD2 - CD2 = 2CD × AD
In the following figure, OP, OQ, and OR are drawn perpendiculars to the sides BC, CA and AB respectively of triangle ABC.
Prove that: AR2 + BP2 + CQ2 = AQ2 + CP2 + BR2

In a quadrilateral ABCD, ∠B = 90° and ∠D = 90°.
Prove that: 2AC2 - AB2 = BC2 + CD2 + DA2
The sides of a certain triangle is given below. Find, which of them is right-triangle
16 cm, 20 cm, and 12 cm
In a right-angled triangle PQR, right-angled at Q, S and T are points on PQ and QR respectively such as PT = SR = 13 cm, QT = 5 cm and PS = TR. Find the length of PQ and PS.
The perimeter of the rectangle whose length is 60 cm and a diagonal is 61 cm is ______.
