Advertisements
Advertisements
Question
In triangle ABC, AB = AC and BD is perpendicular to AC.
Prove that: BD2 - CD2 = 2CD × AD
Solution

In right-angled ΔADB,
BD2 = AB2 + AD2 ...(Pythagoras theorem)
⇒ BD2 = AC2 - AD2
⇒ BD2 = (AD + DC)2 - AD2
⇒ BD2 = AD2 + CD2 + 2AD × DC - AD2
⇒ BD2 - DC2 = 2AD × DC
APPEARS IN
RELATED QUESTIONS
ABCD is a rectangle whose three vertices are B (4, 0), C(4, 3) and D(0,3). The length of one of its diagonals is
(A) 5
(B) 4
(C) 3
(D) 25
ABC is an equilateral triangle of side 2a. Find each of its altitudes.
Prove that the sum of the squares of the sides of a rhombus is equal to the sum of the squares of its diagonals
Two poles of heights 6 m and 11 m stand on a plane ground. If the distance between the feet of the poles is 12 m, find the distance between their tops.
Prove that the sum of the squares of the diagonals of parallelogram is equal to the sum of the squares of its sides.
Find the side and perimeter of a square whose diagonal is 10 cm.
Digonals of parallelogram WXYZ intersect at point O. If OY =5, find WY.
In right angle ΔABC, if ∠B = 90°, AB = 6, BC = 8, then find AC.
In ΔABC, Find the sides of the triangle, if:
- AB = ( x - 3 ) cm, BC = ( x + 4 ) cm and AC = ( x + 6 ) cm
- AB = x cm, BC = ( 4x + 4 ) cm and AC = ( 4x + 5) cm
If the sides of the triangle are in the ratio 1: `sqrt2`: 1, show that is a right-angled triangle.
In triangle ABC, ∠B = 90o and D is the mid-point of BC.
Prove that: AC2 = AD2 + 3CD2.
M andN are the mid-points of the sides QR and PQ respectively of a PQR, right-angled at Q.
Prove that:
(i) PM2 + RN2 = 5 MN2
(ii) 4 PM2 = 4 PQ2 + QR2
(iii) 4 RN2 = PQ2 + 4 QR2(iv) 4 (PM2 + RN2) = 5 PR2
In the figure below, find the value of 'x'.

In a right-angled triangle ABC,ABC = 90°, AC = 10 cm, BC = 6 cm and BC produced to D such CD = 9 cm. Find the length of AD.
In a right-angled triangle PQR, right-angled at Q, S and T are points on PQ and QR respectively such as PT = SR = 13 cm, QT = 5 cm and PS = TR. Find the length of PQ and PS.
Find the length of the support cable required to support the tower with the floor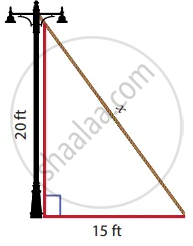
In a right-angled triangle ABC, if angle B = 90°, BC = 3 cm and AC = 5 cm, then the length of side AB is ______.
Two squares are congruent, if they have same ______.
The hypotenuse (in cm) of a right angled triangle is 6 cm more than twice the length of the shortest side. If the length of third side is 6 cm less than thrice the length of shortest side, then find the dimensions of the triangle.
