Advertisements
Advertisements
Question
In a right-angled triangle ABC, if angle B = 90°, BC = 3 cm and AC = 5 cm, then the length of side AB is ______.
Options
3 cm
4 cm
5 cm
6 cm
Solution
In a right-angled triangle ABC, if angle B = 90°, BC = 3 cm and AC = 5 cm, then the length of side AB is 4 cm.
Explanation:
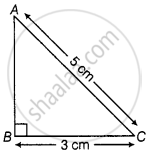
In right angled ΔABC,
AC2 = AB2 + BC2 ......[By Pythagoras theorem]
⇒ 52 = AB2 + 32 ......[∵ AC = 5 cm and BC = 3 cm, given]
⇒ AB2 = 25 – 9
⇒ AB2 = 16
⇒ AB = `sqrt(16)`
⇒ AB = 4 cm
APPEARS IN
RELATED QUESTIONS
Which of the following can be the sides of a right triangle?
1.5 cm, 2 cm, 2.5 cm
In the case of right-angled triangles, identify the right angles.
Find the length of the hypotenuse of a right angled triangle if remaining sides are 9 cm and 12 cm.
In the figure, given below, AD ⊥ BC.
Prove that: c2 = a2 + b2 - 2ax.
In an isosceles triangle ABC; AB = AC and D is the point on BC produced.
Prove that: AD2 = AC2 + BD.CD.
If P and Q are the points on side CA and CB respectively of ΔABC, right angled at C, prove that (AQ2 + BP2 ) = (AB2 + PQ2)
In the given figure, angle ADB = 90°, AC = AB = 26 cm and BD = DC. If the length of AD = 24 cm; find the length of BC.

A ladder, 6.5 m long, rests against a vertical wall. If the foot of the ladder is 2.5 m from the foot of the wall, find up to how much height does the ladder reach?
The sides of the triangle are given below. Find out which one is the right-angled triangle?
11, 12, 15
A 5 m long ladder is placed leaning towards a vertical wall such that it reaches the wall at a point 4 m high. If the foot of the ladder is moved 1.6 m towards the wall, then find the distance by which the top of the ladder would slide upwards on the wall.
Two squares having same perimeter are congruent.
