Question

Prove that the sum of the squares of the diagonals of parallelogram is equal to the sum of the squares of its sides.

Answer 1

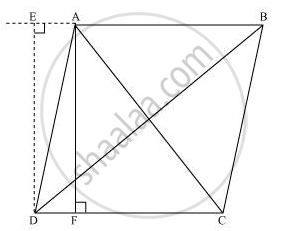
Let ABCD be a parallelogram.

Let us draw perpendicular DE on extended side AB, and AF on side DC.

Applying Pythagoras theorem in ΔDEA, we obtain

DE² + EA² = DA² … (i)

Applying Pythagoras theorem in ΔDEB, we obtain

DE² + EB² = DB²

DE² + (EA + AB)² = DB²

(DE² + EA²) + AB² + 2EA × AB = DB²

DA² + AB² + 2EA × AB = DB² … (ii)

Applying Pythagoras theorem in ΔADF, we obtain

AD² = AF² + FD²

Applying Pythagoras theorem in ΔAFC, we obtain

AC² = AF² + FC²

= AF² + (DC − FD)²

= AF² + DC² + FD² − 2DC × FD

= (AF² + FD²) + DC² − 2DC × FD

AC² = AD² + DC² − 2DC × FD … (iii)

Since ABCD is a parallelogram,

AB = CD … (iv)

And, BC = AD … (v)

In ΔDEA and ΔADF,

∠DEA = ∠AFD (Both 90°)

∠EAD = ∠ADF (EA || DF)

AD = AD (Common)

∴ ΔEAD `~=` ΔFDA (AAS congruence criterion)

⇒ EA = DF … (vi)

Adding equations (i) and (iii), we obtain

DA² + AB² + 2EA × AB + AD² + DC² − 2DC × FD = DB² + AC²

DA² + AB² + AD² + DC² + 2EA × AB − 2DC × FD = DB² + AC²

BC² + AB² + AD² + DC² + 2EA × AB − 2AB × EA = DB² + AC²

[Using equations (iv) and (vi)]

AB² + BC² + CD² + DA² = AC² + BD²