Advertisements
Advertisements
Question
In triangle ABC, ∠B = 90o and D is the mid-point of BC.
Prove that: AC2 = AD2 + 3CD2.
Solution
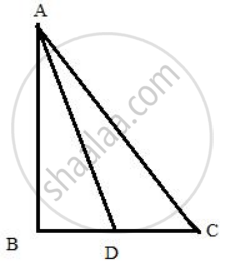
In ΔABC
AB2 + BC2 = AC2
as [BC = 2CD]
AB2 + 4CD2 = AC2 ....(1)
In ΔABD,
AD2 = AB2 + BD2 = AB2 + CD2 ....(2)
Subtracting (1) and (2)
AC2 - AD2 = AB2 + 4CD2 - (AB2 + CD2)
AC2 - AD2 = 3CD2
AC2 = AD2 + 3CD2
Hence proved.
APPEARS IN
RELATED QUESTIONS
If the sides of a triangle are 6 cm, 8 cm and 10 cm, respectively, then determine whether the triangle is a right angle triangle or not.
In Fig., ∆ABC is an obtuse triangle, obtuse angled at B. If AD ⊥ CB, prove that AC2 = AB2 + BC2 + 2BC × BD
The perpendicular AD on the base BC of a ∆ABC intersects BC at D so that DB = 3 CD. Prove that `2"AB"^2 = 2"AC"^2 + "BC"^2`
The diagonals of a rhombus measure 16 cm and 30 cm. Find its perimeter.
In the given figure, ∠B = 90°, XY || BC, AB = 12 cm, AY = 8cm and AX : XB = 1 : 2 = AY : YC.
Find the lengths of AC and BC.

Prove that (1 + cot A - cosec A ) (1 + tan A + sec A) = 2
The sides of a certain triangle is given below. Find, which of them is right-triangle
16 cm, 20 cm, and 12 cm
In the given figure, angle ACP = ∠BDP = 90°, AC = 12 m, BD = 9 m and PA= PB = 15 m. Find:
(i) CP
(ii) PD
(iii) CD

A ladder 15m long reaches a window which is 9m above the ground on one side of a street. Keeping its foot at the same point, the ladder is turned to other side of the street to reach a window 12m high. Find the width of the street.
In an equilateral triangle ABC, the side BC is trisected at D. Prove that 9 AD2 = 7 AB2.
In the given figure. PQ = PS, P =R = 90°. RS = 20 cm and QR = 21 cm. Find the length of PQ correct to two decimal places.
PQR is an isosceles triangle with PQ = PR = 10 cm and QR = 12 cm. Find the length of the perpendicular from P to QR.
To get from point A to point B you must avoid walking through a pond. You must walk 34 m south and 41 m east. To the nearest meter, how many meters would be saved if it were possible to make a way through the pond?
From given figure, In ∆ABC, If AC = 12 cm. then AB =?

Activity: From given figure, In ∆ABC, ∠ABC = 90°, ∠ACB = 30°
∴ ∠BAC = `square`
∴ ∆ABC is 30° – 60° – 90° triangle
∴ In ∆ABC by property of 30° – 60° – 90° triangle.
∴ AB = `1/2` AC and `square` = `sqrt(3)/2` AC
∴ `square` = `1/2 xx 12` and BC = `sqrt(3)/2 xx 12`
∴ `square` = 6 and BC = `6sqrt(3)`
A 5 m long ladder is placed leaning towards a vertical wall such that it reaches the wall at a point 4 m high. If the foot of the ladder is moved 1.6 m towards the wall, then find the distance by which the top of the ladder would slide upwards on the wall.
Two trees 7 m and 4 m high stand upright on a ground. If their bases (roots) are 4 m apart, then the distance between their tops is ______.
In a right-angled triangle ABC, if angle B = 90°, then which of the following is true?
The longest side of a right angled triangle is called its ______.
If the hypotenuse of one right triangle is equal to the hypotenuse of another right triangle, then the triangles are congruent.
The foot of a ladder is 6 m away from its wall and its top reaches a window 8 m above the ground. Find the length of the ladder.
