Advertisements
Advertisements
Question
Two trees 7 m and 4 m high stand upright on a ground. If their bases (roots) are 4 m apart, then the distance between their tops is ______.
Options
3 m
5 m
4 m
11 m
Solution
Two trees 7 m and 4 m high stand upright on a ground. If their bases (roots) are 4 m apart, then the distance between their tops is 5 m.
Explanation:
Let BE be the smaller tree and AD be the bigger tree. Now, we have to find AB (i.e. the distance between their tops).
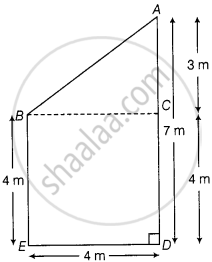
By observing,
ED = BC = 4 m and BE = CD = 4 m
In ΔABC, BC = 4 m
And AC = AD – CD = (7 – 4) m = 3 m
In right angled ΔABC,
AB2 = AC2 + BC2 = 42 + 32 ......[By Pythagoras theorem]
= 16 + 9
⇒ AB2 = 25
⇒ AB = `sqrt(25)`
⇒ AB = 5 m
Therefore, the distance between their tops is 5 m.
APPEARS IN
RELATED QUESTIONS
In a ∆ABC, AD ⊥ BC and AD2 = BC × CD. Prove ∆ABC is a right triangle
In the given figure, ABC is a triangle in which ∠ABC < 90° and AD ⊥ BC. Prove that AC2 = AB2 + BC2 − 2BC.BD.

In ∆ABC, AB = 10, AC = 7, BC = 9, then find the length of the median drawn from point C to side AB.
Find the side of the square whose diagonal is `16sqrt(2)` cm.
A ladder, 6.5 m long, rests against a vertical wall. If the foot of the ladder is 2.5 m from the foot of the wall, find up to how much height does the ladder reach?
If in a ΔPQR, PR2 = PQ2 + QR2, then the right angle of ∆PQR is at the vertex ________
Find the unknown side in the following triangles
A 5 m long ladder is placed leaning towards a vertical wall such that it reaches the wall at a point 4 m high. If the foot of the ladder is moved 1.6 m towards the wall, then find the distance by which the top of the ladder would slide upwards on the wall.
If the areas of two circles are the same, they are congruent.
The foot of a ladder is 6 m away from its wall and its top reaches a window 8 m above the ground. Find the length of the ladder.
