Advertisements
Advertisements
प्रश्न
Two trees 7 m and 4 m high stand upright on a ground. If their bases (roots) are 4 m apart, then the distance between their tops is ______.
विकल्प
3 m
5 m
4 m
11 m
Advertisements
उत्तर
Two trees 7 m and 4 m high stand upright on a ground. If their bases (roots) are 4 m apart, then the distance between their tops is 5 m.
Explanation:
Let BE be the smaller tree and AD be the bigger tree.
Now, we have to find AB (i.e. the distance between their tops).
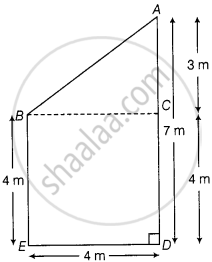
By observing,
ED = BC = 4 m and BE = CD = 4 m
In ΔABC, BC = 4 m
And AC = AD – CD = (7 – 4) m = 3 m
In right angled ΔABC,
AB2 = AC2 + BC2 ...[By Pythagoras theorem]
= 42 + 32
= 16 + 9
⇒ AB2 = 25
⇒ AB = `sqrt(25)`
⇒ AB = 5 m
Therefore, the distance between their tops is 5 m.
APPEARS IN
संबंधित प्रश्न
ABCD is a rectangle whose three vertices are B (4, 0), C(4, 3) and D(0,3). The length of one of its diagonals is
(A) 5
(B) 4
(C) 3
(D) 25
ABC is a right-angled triangle, right-angled at A. A circle is inscribed in it. The lengths of the two sides containing the right angle are 5 cm and 12 cm. Find the radius of the circle
A guy wire attached to a vertical pole of height 18 m is 24 m long and has a stake attached to the other end. How far from the base of the pole should the stake be driven so that the wire will be taut?
The given figure shows a quadrilateral ABCD in which AD = 13 cm, DC = 12 cm, BC = 3 cm and ∠ABD = ∠BCD = 90o. Calculate the length of AB.
M andN are the mid-points of the sides QR and PQ respectively of a PQR, right-angled at Q.
Prove that:
(i) PM2 + RN2 = 5 MN2
(ii) 4 PM2 = 4 PQ2 + QR2
(iii) 4 RN2 = PQ2 + 4 QR2(iv) 4 (PM2 + RN2) = 5 PR2
In the right-angled ∆PQR, ∠ P = 90°. If l(PQ) = 24 cm and l(PR) = 10 cm, find the length of seg QR.
In a triangle ABC right angled at C, P and Q are points of sides CA and CB respectively, which divide these sides the ratio 2 : 1.
Prove that: 9BP2 = 9BC2 + 4AC2
Find the unknown side in the following triangles
Rithika buys an LED TV which has a 25 inches screen. If its height is 7 inches, how wide is the screen? Her TV cabinet is 20 inches wide. Will the TV fit into the cabinet? Give reason
In the given figure, ∠T and ∠B are right angles. If the length of AT, BC and AS (in centimeters) are 15, 16, and 17 respectively, then the length of TC (in centimeters) is ______.
