Advertisements
Advertisements
प्रश्न
If in an isosceles triangle, each of the base angles is 40°, then the triangle is ______.
विकल्प
Right-angled triangle
Acute angled triangle
Obtuse angled triangle
Isosceles right-angled triangle
उत्तर
If in an isosceles triangle, each of the base angles is 40°, then the triangle is obtuse angled triangle.
Explanation:
As we know, the sum of the interior angles of a triangle is 180°.
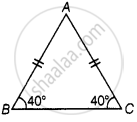
In ΔABC,
∠A + ∠B + ∠C = 180° ......[Angle sum property of a triangle]
⇒ ∠A + 40° + 40° = 180°
⇒ ∠A = 180° – 80°
⇒ ∠A = 100° ......[Obtuse angle]
Therefore, it is an obtuse-angled triangle. Since, it has one angle which is greater than 90°.
APPEARS IN
संबंधित प्रश्न
Find the area of an equilateral triangle of side 20 cm.
Find the perimeter of an equilateral triangle whose area is `16sqrt(3)"cm"`.
Find the area of an equilateral triangle having perimeter of 18cm.
Find the area of the shaded region in the figure as shown, in which DPQS is an equilateral triangle and ∠PQR = 90°.
In a right-angled triangle ABC, if ∠B = 90°, AB - BC = 2 cm; AC - BC = 4 and its perimeter is 24 cm, find the area of the triangle.
Find the area of an isosceles triangle whose perimeter is 72cm and the base is 20cm.
Find the base of an isosceles triangle whose area is 192cm2 and the length of one of the equal sides is 20cm.
Each of the equal sides of an isosceles triangle is 4 cm greater than its height. If the base of the triangle is 24 cm; calculate the perimeter and the area of the triangle.
In an isosceles triangle, angles opposite to equal sides are ______.
Two line segments are congruent, if they are of ______ lengths.
