Advertisements
Advertisements
प्रश्न
In the given figure, ∠DFE = 90°, FG ⊥ ED, If GD = 8, FG = 12, find (1) EG (2) FD and (3) EF

उत्तर
We know that,
In a right angled triangle, the perpendicular segment to the hypotenuse from the opposite vertex, is the geometric mean of the segments into which the hypotenuse is divided.
Here, seg GF ⊥ seg ED
\[\therefore {GF}^2 = EG \times GD\]
\[ \Rightarrow {12}^2 = EG \times 8\]
\[ \Rightarrow 144 = EG \times 8\]
\[ \Rightarrow EG = \frac{144}{8}\]
\[ \Rightarrow EG = 18\]
Hence, EG = 18.
Now,
According to Pythagoras theorem, in ∆DGF
\[{DG}^2 + {GF}^2 = {FD}^2 \]
\[ \Rightarrow 8^2 + {12}^2 = {FD}^2 \]
\[ \Rightarrow 64 + 144 = {FD}^2 \]
\[ \Rightarrow {FD}^2 = 208\]
\[ \Rightarrow FD = 4\sqrt{13}\]
In ∆EGF
\[{EG}^2 + {GF}^2 = {EF}^2 \]
\[ \Rightarrow {18}^2 + {12}^2 = {EF}^2 \]
\[ \Rightarrow 324 + 144 = {EF}^2 \]
\[ \Rightarrow {EF}^2 = 468\]
\[ \Rightarrow EF = 6\sqrt{13}\]
Hence, FD =\[4\sqrt{13}\] and EF=\[6\sqrt{13}\]
संबंधित प्रश्न
In a right triangle ABC, right-angled at B, BC = 12 cm and AB = 5 cm. The radius of the circle inscribed in the triangle (in cm) is
(A) 4
(B) 3
(C) 2
(D) 1
ABC is an isosceles triangle right angled at C. Prove that AB2 = 2AC2
Tick the correct answer and justify: In ΔABC, AB = `6sqrt3` cm, AC = 12 cm and BC = 6 cm.
The angle B is:
A 15 m long ladder reached a window 12 m high from the ground on placing it against a wall at a distance a. Find the distance of the foot of the ladder from the wall.

A man goes 40 m due north and then 50 m due west. Find his distance from the starting point.
In the following figure, AD is perpendicular to BC and D divides BC in the ratio 1: 3.
Prove that : 2AC2 = 2AB2 + BC2
ABC is a triangle, right-angled at B. M is a point on BC.
Prove that: AM2 + BC2 = AC2 + BM2
Diagonals of rhombus ABCD intersect each other at point O.
Prove that: OA2 + OC2 = 2AD2 - `"BD"^2/2`
Find the side of the square whose diagonal is `16sqrt(2)` cm.
A boy first goes 5 m due north and then 12 m due east. Find the distance between the initial and the final position of the boy.
In the figure below, find the value of 'x'.

In the right-angled ∆PQR, ∠ P = 90°. If l(PQ) = 24 cm and l(PR) = 10 cm, find the length of seg QR.
The sides of the triangle are given below. Find out which one is the right-angled triangle?
40, 20, 30
Find the length of the hypotenuse of a triangle whose other two sides are 24cm and 7cm.
Calculate the area of a right-angled triangle whose hypotenuse is 65cm and one side is 16cm.
From a point O in the interior of aΔABC, perpendicular OD, OE and OF are drawn to the sides BC, CA and AB respectively. Prove that: AF2 + BD2 + CE2 = AE2 + CD2 + BF2
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AB2 + AC2 = 2AD2 + `(1)/(2)"BC"^2`
In a right-angled triangle PQR, right-angled at Q, S and T are points on PQ and QR respectively such as PT = SR = 13 cm, QT = 5 cm and PS = TR. Find the length of PQ and PS.
Find the length of the support cable required to support the tower with the floor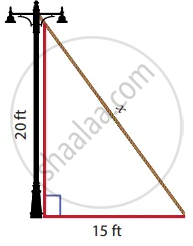
In ∆PQR, PD ⊥ QR such that D lies on QR. If PQ = a, PR = b, QD = c and DR = d, prove that (a + b)(a – b) = (c + d)(c – d).
