Advertisements
Advertisements
प्रश्न
Diagonals of rhombus ABCD intersect each other at point O.
Prove that: OA2 + OC2 = 2AD2 - `"BD"^2/2`
उत्तर
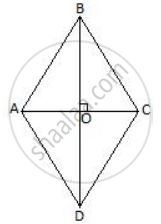
Diagonals of the rhombus are perpendicular to each other.
In quadrilateral ABCD, ∠AOD = ∠COD = 90°.
So, ΔAOD and ΔCOD are right-angled triangles.
In ΔAOD using Pythagoras theorem,
AD2 = OA2 + OD2
⇒ OA2 = AD2 - OD2 ....(i)
In ΔCOD using Pythagoras theorem,
CD2 = OC2 + OD2
⇒ OC2 = CD2 - OD2 ....(ii)
LHS = OA2 + OC2
= AD2 - OD2 + CD2 - OD2 ...[ From(i) and (ii) ]
= AD2 + CD2 - 2OD2
= AD2 + AD2 - 2`("BD"/2)^2` ...[ AD = CD and OD = `"BD"/2`]
= 2AD2 - `("BD")^2/2`
= RHS.
APPEARS IN
संबंधित प्रश्न
In Figure ABD is a triangle right angled at A and AC ⊥ BD. Show that AC2 = BC × DC

In the following figure, O is a point in the interior of a triangle ABC, OD ⊥ BC, OE ⊥ AC and OF ⊥ AB. Show that

(i) OA2 + OB2 + OC2 − OD2 − OE2 − OF2 = AF2 + BD2 + CE2
(ii) AF2 + BD2 + CE2 = AE2 + CD2 + BF2
Two poles of heights 6 m and 11 m stand on a plane ground. If the distance between the feet of the poles is 12 m, find the distance between their tops.
In the given figure, ABC is a triangle in which ∠ABC> 90° and AD ⊥ CB produced. Prove that AC2 = AB2 + BC2 + 2BC.BD.

Which of the following can be the sides of a right triangle?
2.5 cm, 6.5 cm, 6 cm
In the case of right-angled triangles, identify the right angles.
Identify, with reason, if the following is a Pythagorean triplet.
(3, 5, 4)
In ∆PQR, point S is the midpoint of side QR. If PQ = 11, PR = 17, PS = 13, find QR.
In the figure, given below, AD ⊥ BC.
Prove that: c2 = a2 + b2 - 2ax.
In equilateral Δ ABC, AD ⊥ BC and BC = x cm. Find, in terms of x, the length of AD.
In the given figure, AD = 13 cm, BC = 12 cm, AB = 3 cm and angle ACD = angle ABC = 90°. Find the length of DC.

In a triangle ABC right angled at C, P and Q are points of sides CA and CB respectively, which divide these sides the ratio 2 : 1.
Prove that: 9BP2 = 9BC2 + 4AC2
In a triangle ABC right angled at C, P and Q are points of sides CA and CB respectively, which divide these sides the ratio 2 : 1.
Prove that : 9(AQ2 + BP2) = 13AB2
If in a ΔPQR, PR2 = PQ2 + QR2, then the right angle of ∆PQR is at the vertex ________
Find the unknown side in the following triangles
Foot of a 10 m long ladder leaning against a vertical wall is 6 m away from the base of the wall. Find the height of the point on the wall where the top of the ladder reaches.
A 5 m long ladder is placed leaning towards a vertical wall such that it reaches the wall at a point 4 m high. If the foot of the ladder is moved 1.6 m towards the wall, then find the distance by which the top of the ladder would slide upwards on the wall.
A flag pole 18 m high casts a shadow 9.6 m long. Find the distance of the top of the pole from the far end of the shadow.
In figure, PQR is a right triangle right angled at Q and QS ⊥ PR. If PQ = 6 cm and PS = 4 cm, find QS, RS and QR.
The top of a broken tree touches the ground at a distance of 12 m from its base. If the tree is broken at a height of 5 m from the ground then the actual height of the tree is ______.
The longest side of a right angled triangle is called its ______.
