Advertisements
Advertisements
प्रश्न
A flag pole 18 m high casts a shadow 9.6 m long. Find the distance of the top of the pole from the far end of the shadow.
उत्तर
Let BC = 18 m be the flag pole and its shadow be AB = 9.6 m.
The distance of the top of the pole, C from the far end i.e., A of the shadow is AC.
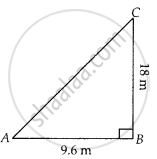
In right angled ∆ABC,
AC2 = AB2 + BC2 ...[By pythagoras theorem]
⇒ AC2 = (9.6)2 + (18)2
⇒ AC2 = 92.16 + 324
⇒ AC2 = 416.16
∴ AC = `sqrt(416.16)` = 20.4 m
Hence, the required distance is 20.4 m.
APPEARS IN
संबंधित प्रश्न
Two poles of heights 6 m and 11 m stand on a plane ground. If the distance between the feet of the poles is 12 m, find the distance between their tops.
In the figure: ∠PSQ = 90o, PQ = 10 cm, QS = 6 cm and RQ = 9 cm. Calculate the length of PR.
In the given figure, ∠B = 90°, XY || BC, AB = 12 cm, AY = 8cm and AX : XB = 1 : 2 = AY : YC.
Find the lengths of AC and BC.

In the following Figure ∠ACB= 90° and CD ⊥ AB, prove that CD2 = BD × AD

If P and Q are the points on side CA and CB respectively of ΔABC, right angled at C, prove that (AQ2 + BP2 ) = (AB2 + PQ2)
In triangle PQR, angle Q = 90°, find: PR, if PQ = 8 cm and QR = 6 cm
In the given figure, angle ADB = 90°, AC = AB = 26 cm and BD = DC. If the length of AD = 24 cm; find the length of BC.

In a right-angled triangle ABC,ABC = 90°, AC = 10 cm, BC = 6 cm and BC produced to D such CD = 9 cm. Find the length of AD.
An isosceles triangle has equal sides each 13 cm and a base 24 cm in length. Find its height
The top of a broken tree touches the ground at a distance of 12 m from its base. If the tree is broken at a height of 5 m from the ground then the actual height of the tree is ______.
