Advertisements
Advertisements
प्रश्न
The top of a broken tree touches the ground at a distance of 12 m from its base. If the tree is broken at a height of 5 m from the ground then the actual height of the tree is ______.
विकल्प
25 m
13 m
18 m
17 m
उत्तर
The top of a broken tree touches the ground at a distance of 12 m from its base. If the tree is broken at a height of 5 m from the ground then the actual height of the tree is 18 m.
Explanation:
Let BC is the broken part of tree and AB is the unbroken part of tree.
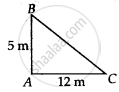
Here, ΔABC is right angled triangle
(BC)2 = (AB)2 + (AC)2
⇒ (BC)2 = (5)2 + (12)2
⇒ (BC)2 = 25 + 144 = 169
⇒ (BC)2 = 132
⇒ BC = 13 m
∴ Actual height of tree is AB + BC = (5 + 13) m = 18 m.
APPEARS IN
संबंधित प्रश्न
P and Q are the mid-points of the sides CA and CB respectively of a ∆ABC, right angled at C. Prove that:
`(i) 4AQ^2 = 4AC^2 + BC^2`
`(ii) 4BP^2 = 4BC^2 + AC^2`
`(iii) (4AQ^2 + BP^2 ) = 5AB^2`
PQR is a triangle right angled at P. If PQ = 10 cm and PR = 24 cm, find QR.
Prove that, in a right-angled triangle, the square of the hypotenuse is equal to the sum of the square of remaining two sides
Identify, with reason, if the following is a Pythagorean triplet.
(4, 9, 12)
In triangle PQR, angle Q = 90°, find: PR, if PQ = 8 cm and QR = 6 cm
Use the information given in the figure to find the length AD.

In an equilateral triangle ABC, the side BC is trisected at D. Prove that 9 AD2 = 7 AB2.
In a square PQRS of side 5 cm, A, B, C and D are points on sides PQ, QR, RS and SP respectively such as PA = PD = RB = RC = 2 cm. Prove that ABCD is a rectangle. Also, find the area and perimeter of the rectangle.
A 5 m long ladder is placed leaning towards a vertical wall such that it reaches the wall at a point 4 m high. If the foot of the ladder is moved 1.6 m towards the wall, then find the distance by which the top of the ladder would slide upwards on the wall.
Two trees 7 m and 4 m high stand upright on a ground. If their bases (roots) are 4 m apart, then the distance between their tops is ______.
