Advertisements
Advertisements
प्रश्न
The top of a broken tree touches the ground at a distance of 12 m from its base. If the tree is broken at a height of 5 m from the ground then the actual height of the tree is ______.
पर्याय
25 m
13 m
18 m
17 m
उत्तर
The top of a broken tree touches the ground at a distance of 12 m from its base. If the tree is broken at a height of 5 m from the ground then the actual height of the tree is 18 m.
Explanation:
Let BC is the broken part of tree and AB is the unbroken part of tree.
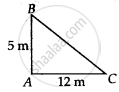
Here, ΔABC is right angled triangle
(BC)2 = (AB)2 + (AC)2
⇒ (BC)2 = (5)2 + (12)2
⇒ (BC)2 = 25 + 144 = 169
⇒ (BC)2 = 132
⇒ BC = 13 m
∴ Actual height of tree is AB + BC = (5 + 13) m = 18 m.
APPEARS IN
संबंधित प्रश्न
Sides of triangle are given below. Determine it is a right triangle or not? In case of a right triangle, write the length of its hypotenuse. 50 cm, 80 cm, 100 cm
Prove that the points A(0, −1), B(−2, 3), C(6, 7) and D(8, 3) are the vertices of a rectangle ABCD?
Identify, with reason, if the following is a Pythagorean triplet.
(4, 9, 12)
In the following Figure ∠ACB= 90° and CD ⊥ AB, prove that CD2 = BD × AD

Choose the correct alternative:
In right-angled triangle PQR, if hypotenuse PR = 12 and PQ = 6, then what is the measure of ∠P?
Each side of rhombus is 10cm. If one of its diagonals is 16cm, find the length of the other diagonals.
∆ABC is right-angled at C. If AC = 5 cm and BC = 12 cm. find the length of AB.
In triangle ABC, line I, is a perpendicular bisector of BC.
If BC = 12 cm, SM = 8 cm, find CS
From given figure, In ∆ABC, If AC = 12 cm. then AB =?

Activity: From given figure, In ∆ABC, ∠ABC = 90°, ∠ACB = 30°
∴ ∠BAC = `square`
∴ ∆ABC is 30° – 60° – 90° triangle
∴ In ∆ABC by property of 30° – 60° – 90° triangle.
∴ AB = `1/2` AC and `square` = `sqrt(3)/2` AC
∴ `square` = `1/2 xx 12` and BC = `sqrt(3)/2 xx 12`
∴ `square` = 6 and BC = `6sqrt(3)`
Prove that the area of the equilateral triangle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the equilateral triangles drawn on the other two sides of the triangle.
