Advertisements
Advertisements
प्रश्न
Prove that the points A(0, −1), B(−2, 3), C(6, 7) and D(8, 3) are the vertices of a rectangle ABCD?
उत्तर
Let the points (0, −1), (−2, 3), (6, 7), and (8, 3) be representing the vertices A, B, C, and D of a quadrilateral respectively.
Distance between the two points (x1, y1) and (x2, y2) is given by`sqrt((x_2-x_1)^2+(y_2-Y_1)^2)`
`thereforeAB=sqrt((0-(-2))^2+(-1-3)^2)``=sqrt((2)^2+(-4)^2)``=sqrt(4+16)=sqrt20=2sqrt5`
`BC=sqrt((-2-6)^2+(3-7)^2)=sqrt((-8)^2+(-4)^2)=sqrt64+16=sqrt80=4sqrt5`
`CD=sqrt((6-8)^2+(7-3)^2)=sqrt((-2)^2+(4)^2)=sqrt(4+16)=sqrt20=2sqrt5`
`AD=sqrt((8-0)^2+(3-(-1)^2))=sqrt((8)^2+(-8)^2)=sqrt64+16=sqrt80=4sqrt5`
Diagonal AC=`sqrt((0-6)^2+(-1-7)^2)=sqrt(6^2+(-8)^2)=sqrt100=10`
Diagonal AC=`sqrt((-2-8)^2+(3-3)^2)=sqrt((-10)^2+0^2)=sqrt100=10`
It can be observed that opposite sides of this quadrilateral are of the same length and also, the diagonals are of the same length.
Therefore, the given points are the vertices of a rectangle.
APPEARS IN
संबंधित प्रश्न
Prove that the sum of the squares of the sides of a rhombus is equal to the sum of the squares of its diagonals
Which of the following can be the sides of a right triangle?
2 cm, 2 cm, 5 cm
In the case of right-angled triangles, identify the right angles.
Identify, with reason, if the following is a Pythagorean triplet.
(5, 12, 13)
In the given figure, AB//CD, AB = 7 cm, BD = 25 cm and CD = 17 cm;
find the length of side BC.
Find the Pythagorean triplet from among the following set of numbers.
2, 4, 5
Find the length of the support cable required to support the tower with the floor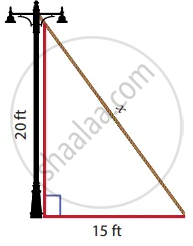
A flag pole 18 m high casts a shadow 9.6 m long. Find the distance of the top of the pole from the far end of the shadow.
The perimeter of the rectangle whose length is 60 cm and a diagonal is 61 cm is ______.
Two squares having same perimeter are congruent.
Jayanti takes shortest route to her home by walking diagonally across a rectangular park. The park measures 60 metres × 80 metres. How much shorter is the route across the park than the route around its edges?
