Advertisements
Advertisements
Question
The top of a broken tree touches the ground at a distance of 12 m from its base. If the tree is broken at a height of 5 m from the ground then the actual height of the tree is ______.
Options
25 m
13 m
18 m
17 m
Solution
The top of a broken tree touches the ground at a distance of 12 m from its base. If the tree is broken at a height of 5 m from the ground then the actual height of the tree is 18 m.
Explanation:
Let BC is the broken part of tree and AB is the unbroken part of tree.
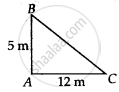
Here, ΔABC is right angled triangle
(BC)2 = (AB)2 + (AC)2
⇒ (BC)2 = (5)2 + (12)2
⇒ (BC)2 = 25 + 144 = 169
⇒ (BC)2 = 132
⇒ BC = 13 m
∴ Actual height of tree is AB + BC = (5 + 13) m = 18 m.
APPEARS IN
RELATED QUESTIONS
ABCD is a rectangle whose three vertices are B (4, 0), C(4, 3) and D(0,3). The length of one of its diagonals is
(A) 5
(B) 4
(C) 3
(D) 25
Sides of triangle are given below. Determine it is a right triangle or not? In case of a right triangle, write the length of its hypotenuse. 50 cm, 80 cm, 100 cm
Prove that the points A(0, −1), B(−2, 3), C(6, 7) and D(8, 3) are the vertices of a rectangle ABCD?
In triangle ABC, AB = AC and BD is perpendicular to AC.
Prove that: BD2 - CD2 = 2CD × AD
ABC is a triangle, right-angled at B. M is a point on BC.
Prove that: AM2 + BC2 = AC2 + BM2
The sides of a certain triangle is given below. Find, which of them is right-triangle
16 cm, 20 cm, and 12 cm
A ladder 15m long reaches a window which is 9m above the ground on one side of a street. Keeping its foot at the same point, the ladder is turned to other side of the street to reach a window 12m high. Find the width of the street.
Is the triangle with sides 25 cm, 5 cm and 24 cm a right triangle? Give reasons for your answer.
Prove that the area of the semicircle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the semicircles drawn on the other two sides of the triangle.
A right-angled triangle may have all sides equal.
