Advertisements
Advertisements
प्रश्न
Prove that, in a right-angled triangle, the square of the hypotenuse is equal to the sum of the square of remaining two sides
उत्तर
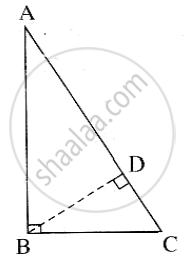
Draw perpendicular BD from the vertex B to the side AC. A - D
In right-angled `triangle ABC`
seg BD ⊥ hypotenuse AC.
∴ by the similarity in right-angled triangles
`triangle ABC ~ triangle ADB ~ triangle BDC`
Now, `triangle ABC ~ triangle ADB`
`:. (AB)/(AD) = (AC)/(AB) ` ......(c.s.s.t)
∴ AB2 = AC x AD ......(1)
Also, `triangleABC ~ triangleBDC`
`:. (BC)/(DC) = (AC)/(BC)` ......(c.s.s.t)
`:. BC^2 = AC xx DC` ......(2)
From (1) and (2),
`AB^2 + BC^2 = AC xx AD + AC xx DC`
`= AC xx (AD + DC)`
`= AC xx AC` ......(A-D-C)
`:. AB^2 + BC^2 = AC^2`
`i.e, AC^2 = AB^2 + BC^2`
APPEARS IN
संबंधित प्रश्न
In triangle ABC, ∠C=90°. Let BC= a, CA= b, AB= c and let 'p' be the length of the perpendicular from 'C' on AB, prove that:
1. cp = ab
2. `1/p^2=1/a^2+1/b^2`
Two towers of heights 10 m and 30 m stand on a plane ground. If the distance between their feet is 15 m, find the distance between their tops
P and Q are the mid-points of the sides CA and CB respectively of a ∆ABC, right angled at C. Prove that:
`(i) 4AQ^2 = 4AC^2 + BC^2`
`(ii) 4BP^2 = 4BC^2 + AC^2`
`(iii) (4AQ^2 + BP^2 ) = 5AB^2`
Sides of triangle are given below. Determine it is a right triangle or not? In case of a right triangle, write the length of its hypotenuse. 13 cm, 12 cm, 5 cm
ABC is an isosceles triangle right angled at C. Prove that AB2 = 2AC2
D and E are points on the sides CA and CB respectively of a triangle ABC right angled at C. Prove that AE2 + BD2 = AB2 + DE2
In the given figure, AD is a median of a triangle ABC and AM ⊥ BC. Prove that:
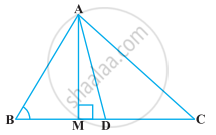
`"AC"^2 = "AD"^2 + "BC"."DM" + (("BC")/2)^2`
In the given figure, point T is in the interior of rectangle PQRS, Prove that, TS2 + TQ2 = TP2 + TR2 (As shown in the figure, draw seg AB || side SR and A-T-B)

In equilateral Δ ABC, AD ⊥ BC and BC = x cm. Find, in terms of x, the length of AD.
In ∆ ABC, AD ⊥ BC.
Prove that AC2 = AB2 +BC2 − 2BC x BD
Find the length of the perpendicular of a triangle whose base is 5cm and the hypotenuse is 13cm. Also, find its area.
The foot of a ladder is 6m away from a wall and its top reaches a window 8m above the ground. If the ladder is shifted in such a way that its foot is 8m away from the wall to what height does its tip reach?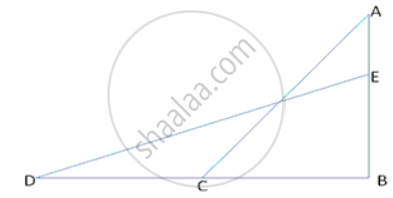
Two poles of height 9m and 14m stand on a plane ground. If the distance between their 12m, find the distance between their tops.
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AC2 = AD2 + BC x DE + `(1)/(4)"BC"^2`
Two trains leave a railway station at the same time. The first train travels due west and the second train due north. The first train travels at a speed of `(20 "km")/"hr"` and the second train travels at `(30 "km")/"hr"`. After 2 hours, what is the distance between them?
In a right angled triangle, if length of hypotenuse is 25 cm and height is 7 cm, then what is the length of its base?
In ΔABC, if DE || BC, AD = x, DB = x – 2, AE = x + 2 and EC = x – 1, then value of x is ______.
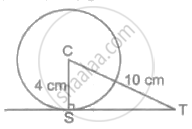
In the adjoining figure, a tangent is drawn to a circle of radius 4 cm and centre C, at the point S. Find the length of the tangent ST, if CT = 10 cm.
Two rectangles are congruent, if they have same ______ and ______.
