Advertisements
Advertisements
Question
Prove that, in a right-angled triangle, the square of the hypotenuse is equal to the sum of the square of remaining two sides
Solution
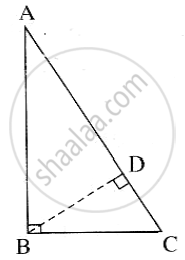
Draw perpendicular BD from the vertex B to the side AC. A - D
In right-angled `triangle ABC`
seg BD ⊥ hypotenuse AC.
∴ by the similarity in right-angled triangles
`triangle ABC ~ triangle ADB ~ triangle BDC`
Now, `triangle ABC ~ triangle ADB`
`:. (AB)/(AD) = (AC)/(AB) ` ......(c.s.s.t)
∴ AB2 = AC x AD ......(1)
Also, `triangleABC ~ triangleBDC`
`:. (BC)/(DC) = (AC)/(BC)` ......(c.s.s.t)
`:. BC^2 = AC xx DC` ......(2)
From (1) and (2),
`AB^2 + BC^2 = AC xx AD + AC xx DC`
`= AC xx (AD + DC)`
`= AC xx AC` ......(A-D-C)
`:. AB^2 + BC^2 = AC^2`
`i.e, AC^2 = AB^2 + BC^2`
APPEARS IN
RELATED QUESTIONS
The points A(4, 7), B(p, 3) and C(7, 3) are the vertices of a right traingle ,right-angled at B. Find the values of p.
The perpendicular from A on side BC of a Δ ABC intersects BC at D such that DB = 3CD . Prove that 2AB2 = 2AC2 + BC2.

AD is drawn perpendicular to base BC of an equilateral triangle ABC. Given BC = 10 cm, find the length of AD, correct to 1 place of decimal.
O is any point inside a rectangle ABCD.
Prove that: OB2 + OD2 = OC2 + OA2.
In a quadrilateral ABCD, ∠B = 90° and ∠D = 90°.
Prove that: 2AC2 - AB2 = BC2 + CD2 + DA2
Find the value of (sin2 33 + sin2 57°)
Triangle XYZ is right-angled at vertex Z. Calculate the length of YZ, if XY = 13 cm and XZ = 12 cm.
Triangle PQR is right-angled at vertex R. Calculate the length of PR, if: PQ = 34 cm and QR = 33.6 cm.
The sides of a certain triangle is given below. Find, which of them is right-triangle
6 m, 9 m, and 13 m
In the figure below, find the value of 'x'.

Calculate the area of a right-angled triangle whose hypotenuse is 65cm and one side is 16cm.
In ΔABC, AD is perpendicular to BC. Prove that: AB2 + CD2 = AC2 + BD2
In a triangle ABC right angled at C, P and Q are points of sides CA and CB respectively, which divide these sides the ratio 2 : 1.
Prove that: 9BP2 = 9BC2 + 4AC2
In the given figure, PQ = `"RS"/(3)` = 8cm, 3ST = 4QT = 48cm.
SHow that ∠RTP = 90°.
In ΔABC, if DE || BC, AD = x, DB = x – 2, AE = x + 2 and EC = x – 1, then value of x is ______.
Prove that the area of the equilateral triangle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the equilateral triangles drawn on the other two sides of the triangle.
The top of a broken tree touches the ground at a distance of 12 m from its base. If the tree is broken at a height of 5 m from the ground then the actual height of the tree is ______.
Two angles are said to be ______, if they have equal measures.
In a triangle, sum of squares of two sides is equal to the square of the third side.
Jayanti takes shortest route to her home by walking diagonally across a rectangular park. The park measures 60 metres × 80 metres. How much shorter is the route across the park than the route around its edges?
