Advertisements
Advertisements
प्रश्न
Prove that, in a right-angled triangle, the square of the hypotenuse is equal to the sum of the square of remaining two sides
उत्तर
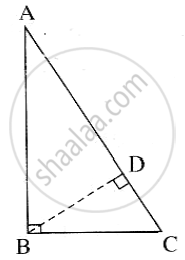
Draw perpendicular BD from the vertex B to the side AC. A - D
In right-angled `triangle ABC`
seg BD ⊥ hypotenuse AC.
∴ by the similarity in right-angled triangles
`triangle ABC ~ triangle ADB ~ triangle BDC`
Now, `triangle ABC ~ triangle ADB`
`:. (AB)/(AD) = (AC)/(AB) ` ......(c.s.s.t)
∴ AB2 = AC x AD ......(1)
Also, `triangleABC ~ triangleBDC`
`:. (BC)/(DC) = (AC)/(BC)` ......(c.s.s.t)
`:. BC^2 = AC xx DC` ......(2)
From (1) and (2),
`AB^2 + BC^2 = AC xx AD + AC xx DC`
`= AC xx (AD + DC)`
`= AC xx AC` ......(A-D-C)
`:. AB^2 + BC^2 = AC^2`
`i.e, AC^2 = AB^2 + BC^2`
APPEARS IN
संबंधित प्रश्न
If the sides of a triangle are 6 cm, 8 cm and 10 cm, respectively, then determine whether the triangle is a right angle triangle or not.
Find the side and perimeter of a square whose diagonal is 10 cm.
In the given figure, M is the midpoint of QR. ∠PRQ = 90°. Prove that, PQ2 = 4PM2 – 3PR2.

In ∆ABC, seg AD ⊥ seg BC, DB = 3CD.
Prove that: 2AB2 = 2AC2 + BC2

Find the value of (sin2 33 + sin2 57°)
If P and Q are the points on side CA and CB respectively of ΔABC, right angled at C, prove that (AQ2 + BP2 ) = (AB2 + PQ2)
In the given figure, angle BAC = 90°, AC = 400 m, and AB = 300 m. Find the length of BC.

In the given figure, AD = 13 cm, BC = 12 cm, AB = 3 cm and angle ACD = angle ABC = 90°. Find the length of DC.

Find the Pythagorean triplet from among the following set of numbers.
3, 4, 5
The sides of the triangle are given below. Find out which one is the right-angled triangle?
8, 15, 17
A ladder 25m long reaches a window of a building 20m above the ground. Determine the distance of the foot of the ladder from the building.
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AB2 + AC2 = 2AD2 + `(1)/(2)"BC"^2`
In a triangle ABC right angled at C, P and Q are points of sides CA and CB respectively, which divide these sides the ratio 2 : 1.
Prove that: 9BP2 = 9BC2 + 4AC2
The perpendicular PS on the base QR of a ∆PQR intersects QR at S, such that QS = 3 SR. Prove that 2PQ2 = 2PR2 + QR2
Two trains leave a railway station at the same time. The first train travels due west and the second train due north. The first train travels at a speed of `(20 "km")/"hr"` and the second train travels at `(30 "km")/"hr"`. After 2 hours, what is the distance between them?
Find the unknown side in the following triangles
Sides AB and BE of a right triangle, right-angled at B are of lengths 16 cm and 8 cm respectively. The length of the side of largest square FDGB that can be inscribed in the triangle ABE is ______.

Prove that the area of the semicircle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the semicircles drawn on the other two sides of the triangle.
In a right-angled triangle ABC, if angle B = 90°, BC = 3 cm and AC = 5 cm, then the length of side AB is ______.
If two legs of a right triangle are equal to two legs of another right triangle, then the right triangles are congruent.
