Advertisements
Advertisements
Question
In a quadrilateral ABCD, ∠B = 90° and ∠D = 90°.
Prove that: 2AC2 - AB2 = BC2 + CD2 + DA2
Solution
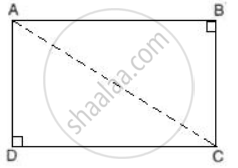
In quadrilateral ABCD, ∠B = 90° and ∠D = 90°.
So, ΔABC and ΔADC are right-angled triangles.
In ΔABC, using Pythagoras theorem,
AC2 = AB2 + BC2
⇒ AB2 = AC2 - BC2 ....(i)
In ΔADC, using Pythagoras theorem,
AC2 = AD2 + DC2 ....(ii)
LHS = 2AC2 - AB2
= 2AC2 - ( AC2 - BC2 ) .....[ From(i) ]
= 2AC2 - AC2 + BC2
= AC2 + BC2
= AD2 + DC2 + BC2 ....[ From(ii) ]
= RHS
APPEARS IN
RELATED QUESTIONS
In a right triangle ABC, right-angled at B, BC = 12 cm and AB = 5 cm. The radius of the circle inscribed in the triangle (in cm) is
(A) 4
(B) 3
(C) 2
(D) 1
D and E are points on the sides CA and CB respectively of a triangle ABC right angled at C. Prove that AE2 + BD2 = AB2 + DE2
In an equilateral triangle, prove that three times the square of one side is equal to four times the square of one of its altitudes.
Prove that the points A(0, −1), B(−2, 3), C(6, 7) and D(8, 3) are the vertices of a rectangle ABCD?
Some question and their alternative answer are given. Select the correct alternative.
If a, b, and c are sides of a triangle and a2 + b2 = c2, name the type of triangle.

In ΔMNP, ∠MNP = 90˚, seg NQ ⊥ seg MP, MQ = 9, QP = 4, find NQ.
In triangle ABC, given below, AB = 8 cm, BC = 6 cm and AC = 3 cm. Calculate the length of OC.

In triangle PQR, angle Q = 90°, find: PR, if PQ = 8 cm and QR = 6 cm
In triangle PQR, angle Q = 90°, find: PQ, if PR = 34 cm and QR = 30 cm
A ladder, 6.5 m long, rests against a vertical wall. If the foot of the ladder is 2.5 m from the foot of the wall, find up to how much height does the ladder reach?
Find the length of the perpendicular of a triangle whose base is 5cm and the hypotenuse is 13cm. Also, find its area.
In a triangle ABC right angled at C, P and Q are points of sides CA and CB respectively, which divide these sides the ratio 2 : 1.
Prove that : 9(AQ2 + BP2) = 13AB2
The hypotenuse of a right angled triangle of sides 12 cm and 16 cm is __________
Find the length of the support cable required to support the tower with the floor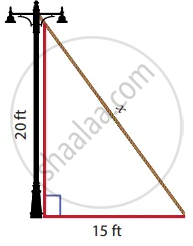
Is the triangle with sides 25 cm, 5 cm and 24 cm a right triangle? Give reasons for your answer.
In a quadrilateral ABCD, ∠A + ∠D = 90°. Prove that AC2 + BD2 = AD2 + BC2
[Hint: Produce AB and DC to meet at E.]
Prove that the area of the semicircle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the semicircles drawn on the other two sides of the triangle.
If two legs of a right triangle are equal to two legs of another right triangle, then the right triangles are congruent.
Jiya walks 6 km due east and then 8 km due north. How far is she from her starting place?
