Advertisements
Advertisements
प्रश्न
In the given figure, point T is in the interior of rectangle PQRS, Prove that, TS2 + TQ2 = TP2 + TR2 (As shown in the figure, draw seg AB || side SR and A-T-B)

उत्तर १
Construction: Through T, draw seg AB II side SR such that A-T-B, P- A-S and Q-B-R.
Proof:
seg PS || seg QR ...(Opposite sides of rectangle)
∴ seg AS || seg BR ...(P-A-S and Q-B-R)
also seg AB || seg SR ...(Construction)
∴ `square` ASRB is a parallelogram ...((By definition)
∠ASR = 90° ...(Angle of rectangle PSRQ)
∴ `square` ASRB is a rectangle ...(A parallelogram is a rectangle, if one of its angles is a right angle.)
∠SAB = ∠ABR = 90° ...(Angle of a rectangle)
∴ seg TA ⊥ side PS and seg TB ⊥ side QR ...(1)
AS = BR ...(2) (Opposite sides of rectangle are equal)
Similarly, we can prove AP= BQ ...(3)
In ΔTAS,
∠TAS = 90° ...[From (1)]
∴ by Pythagoras theorem,
TS2 = TA2 + AS2 ...(4)
In ΔTBQ,
∠TBQ = 90° ...[From (1)]
∴ by Pythagoras theorem,
TQ2 = TB2 + BQ2 ...(5)
Adding (4) and (5), we get,
TS2 + TQ2 = TA2 + AS2 + TB2 + BQ2 ...(6)
In ΔTAP,
∠TAP = 90° ...[From (1)]
∴ by Pythagoras theorem,
TP2 = TA2 + AP2 ...(7)
In ΔTBR,
∠TBR = 90° ...[From (1)]
∴ by Pythagoras theorem,
TR2 = TB2 + BR2 ...(8)
Adding (7) and (8), we get
TP2 + TR2 = TA2 + AP2 + TB2 + BR2
∴ TP2 + TR2 = TA2 + BQ2 + TB2 + AS2 ...(9) [From (2) and (3)]
∴ from (6) and (g), we get,
TS2 + TQ2 = TP2 + TR2
उत्तर २
Construction: Draw diagonals PR and QS and let them intersect at 0. Draw seg TO.
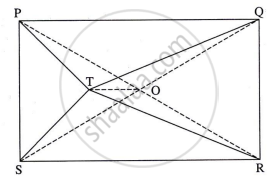
Proof: `square` PQRS is a rectangle ...(Given)
∴ PR=QS ...(Diagonals of rectangle are congruent)
Multiplying both the sides by `1/2`, we get,
`1/2`PR = `1/2`QS ...(1)
But, `1/2`PR = OP = OR ...(2)
and `1/2`QS = OS = OQ ...(3) [Diagonals of rectangle bisect each other]
∴ OP = OR = OS = OQ ...(4) [From (1), (2) and (3)]
In ΔTSQ,
seg TO is the median ...(By definition)
∴ by Apollonius theorem,
TS2 + TQ2 = 2TO2 + 2OQ2 ...(5)
In ΔPTR,
seg TO is the median ...(By definition)
∴ by Apollonius theorem,
TP2 + TR2 = 2TO2 + 2OR2
∴ TP2 + TR2 = 2TO2 + 2OQ2 ...(6) [From (4)]
∴ from (5) and (6), we get,
TS2 + TQ2 = TP2 + TR2
Notes
Students can refer to the provided solutions based on their preferred marks.
संबंधित प्रश्न
In a right triangle ABC, right-angled at B, BC = 12 cm and AB = 5 cm. The radius of the circle inscribed in the triangle (in cm) is
(A) 4
(B) 3
(C) 2
(D) 1
A ladder leaning against a wall makes an angle of 60° with the horizontal. If the foot of the ladder is 2.5 m away from the wall, find the length of the ladder
P and Q are the mid-points of the sides CA and CB respectively of a ∆ABC, right angled at C. Prove that:
`(i) 4AQ^2 = 4AC^2 + BC^2`
`(ii) 4BP^2 = 4BC^2 + AC^2`
`(iii) (4AQ^2 + BP^2 ) = 5AB^2`
From a point O in the interior of a ∆ABC, perpendicular OD, OE and OF are drawn to the sides BC, CA and AB respectively. Prove
that :
`(i) AF^2 + BD^2 + CE^2 = OA^2 + OB^2 + OC^2 – OD^2 – OE^2 – OF^2`
`(ii) AF^2 + BD^2 + CE^2 = AE^2 + CD^2 + BF^2`
An aeroplane leaves an airport and flies due north at a speed of 1,000 km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1,200 km per hour. How far apart will be the two planes after `1 1/2` hours?
Which of the following can be the sides of a right triangle?
1.5 cm, 2 cm, 2.5 cm
In the case of right-angled triangles, identify the right angles.
In the given figure, ∆ABC is an equilateral triangle of side 3 units. Find the coordinates of the other two vertices ?

Find the length of the hypotenuse of a right angled triangle if remaining sides are 9 cm and 12 cm.
In ∆ABC, ∠BAC = 90°, seg BL and seg CM are medians of ∆ABC. Then prove that:
4(BL2 + CM2) = 5 BC2

In equilateral Δ ABC, AD ⊥ BC and BC = x cm. Find, in terms of x, the length of AD.
Show that the triangle ABC is a right-angled triangle; if: AB = 9 cm, BC = 40 cm and AC = 41 cm
Find the Pythagorean triplet from among the following set of numbers.
2, 4, 5
There are two paths that one can choose to go from Sarah’s house to James's house. One way is to take C street, and the other way requires to take B street and then A street. How much shorter is the direct path along C street?

Find the unknown side in the following triangles
Sides AB and BE of a right triangle, right-angled at B are of lengths 16 cm and 8 cm respectively. The length of the side of largest square FDGB that can be inscribed in the triangle ABE is ______.

In an isosceles triangle PQR, the length of equal sides PQ and PR is 13 cm and base QR is 10 cm. Find the length of perpendicular bisector drawn from vertex P to side QR.
In an equilateral triangle PQR, prove that PS2 = 3(QS)2.

Two squares having same perimeter are congruent.
Jayanti takes shortest route to her home by walking diagonally across a rectangular park. The park measures 60 metres × 80 metres. How much shorter is the route across the park than the route around its edges?
Points A and B are on the opposite edges of a pond as shown in figure. To find the distance between the two points, the surveyor makes a right-angled triangle as shown. Find the distance AB.

