Advertisements
Advertisements
प्रश्न
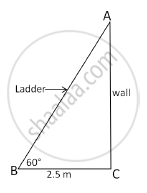
A ladder leaning against a wall makes an angle of 60° with the horizontal. If the foot of the ladder is 2.5 m away from the wall, find the length of the ladder
उत्तर
Let AB be the ladder and CA be the wall.
The ladder makes an angle of 60° with the horizontal.
∴ΔABC is a 30°-60°-90°, right triangle.
Given: BC = 2.5 m, ∠ABC = 60°
∴AB = 5 cm and ∠BAC = 30°
From Pythagoras Theorem, we have
AB2 = BC2 + CA2
∴52 = (2.5)2 + (CA)2
∴(CA)2 = 25 – 6.25 = 18.75 m
Hence, length of the ladder is `sqrt18.75~~4.33m`
APPEARS IN
संबंधित प्रश्न
Prove that the diagonals of a rectangle ABCD, with vertices A(2, -1), B(5, -1), C(5, 6) and D(2, 6), are equal and bisect each other.
Two towers of heights 10 m and 30 m stand on a plane ground. If the distance between their feet is 15 m, find the distance between their tops
Sides of triangles are given below. Determine it is a right triangles? In case of a right triangle, write the length of its hypotenuse. 3 cm, 8 cm, 6 cm
In the given figure, ABC is a triangle in which ∠ABC> 90° and AD ⊥ CB produced. Prove that AC2 = AB2 + BC2 + 2BC.BD.

AD is drawn perpendicular to base BC of an equilateral triangle ABC. Given BC = 10 cm, find the length of AD, correct to 1 place of decimal.
Find the value of (sin2 33 + sin2 57°)
Calculate the area of a right-angled triangle whose hypotenuse is 65cm and one side is 16cm.
From the given figure, in ∆ABQ, if AQ = 8 cm, then AB =?

In an equilateral triangle PQR, prove that PS2 = 3(QS)2.

Jayanti takes shortest route to her home by walking diagonally across a rectangular park. The park measures 60 metres × 80 metres. How much shorter is the route across the park than the route around its edges?
