Advertisements
Advertisements
प्रश्न
Calculate the area of a right-angled triangle whose hypotenuse is 65cm and one side is 16cm.
उत्तर
Hypotenuse = 65cm
One side = 16cm
Let the other side be of length x cm
By Pythagoras theorem,
(65cm)2 = (16cm)2 + (x cm)2
(x cm)2 = 4225cm2 - 256cm2
= 3969cm2
= (63cm)2
⇒ x = 63cm
Area of the triangle
=
=
= 504cm2.
APPEARS IN
संबंधित प्रश्न
ABCD is a rectangle whose three vertices are B (4, 0), C(4, 3) and D(0,3). The length of one of its diagonals is
(A) 5
(B) 4
(C) 3
(D) 25
ABC is an equilateral triangle of side 2a. Find each of its altitudes.
In the given figure, ABC is a triangle in which ∠ABC < 90° and AD ⊥ BC. Prove that AC2 = AB2 + BC2 − 2BC.BD.

Identify, with reason, if the following is a Pythagorean triplet.
(24, 70, 74)
In the given figure, ∠B = 90°, XY || BC, AB = 12 cm, AY = 8cm and AX : XB = 1 : 2 = AY : YC.
Find the lengths of AC and BC.

In the following figure, AD is perpendicular to BC and D divides BC in the ratio 1: 3.
Prove that : 2AC2 = 2AB2 + BC2
In the figure, given below, AD ⊥ BC.
Prove that: c2 = a2 + b2 - 2ax.
Diagonals of rhombus ABCD intersect each other at point O.
Prove that: OA2 + OC2 = 2AD2 -
In the given figure, BL and CM are medians of a ∆ABC right-angled at A. Prove that 4 (BL2 + CM2) = 5 BC2.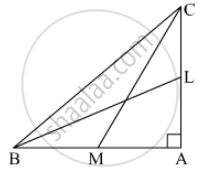
Triangle ABC is right-angled at vertex A. Calculate the length of BC, if AB = 18 cm and AC = 24 cm.
Triangle PQR is right-angled at vertex R. Calculate the length of PR, if: PQ = 34 cm and QR = 33.6 cm.
In triangle PQR, angle Q = 90°, find: PQ, if PR = 34 cm and QR = 30 cm
In the given figure, angle ADB = 90°, AC = AB = 26 cm and BD = DC. If the length of AD = 24 cm; find the length of BC.

A ladder 25m long reaches a window of a building 20m above the ground. Determine the distance of the foot of the ladder from the building.
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AB2 + AC2 = 2AD2 +
Find the length of the support cable required to support the tower with the floor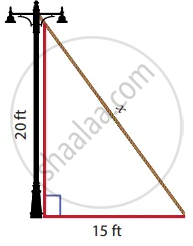
The top of a broken tree touches the ground at a distance of 12 m from its base. If the tree is broken at a height of 5 m from the ground then the actual height of the tree is ______.
In a right-angled triangle ABC, if angle B = 90°, BC = 3 cm and AC = 5 cm, then the length of side AB is ______.
If the areas of two circles are the same, they are congruent.
Two circles having same circumference are congruent.
