Advertisements
Advertisements
प्रश्न
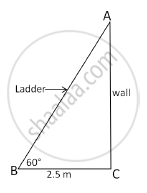
A ladder leaning against a wall makes an angle of 60° with the horizontal. If the foot of the ladder is 2.5 m away from the wall, find the length of the ladder
उत्तर
Let AB be the ladder and CA be the wall.
The ladder makes an angle of 60° with the horizontal.
∴ΔABC is a 30°-60°-90°, right triangle.
Given: BC = 2.5 m, ∠ABC = 60°
∴AB = 5 cm and ∠BAC = 30°
From Pythagoras Theorem, we have
AB2 = BC2 + CA2
∴52 = (2.5)2 + (CA)2
∴(CA)2 = 25 – 6.25 = 18.75 m
Hence, length of the ladder is `sqrt18.75~~4.33m`
APPEARS IN
संबंधित प्रश्न
Side of a triangle is given, determine it is a right triangle.
`(2a – 1) cm, 2\sqrt { 2a } cm, and (2a + 1) cm`
A tree is broken at a height of 5 m from the ground and its top touches the ground at a distance of 12 m from the base of the tree. Find the original height of the tree.
Identify, with reason, if the following is a Pythagorean triplet.
(4, 9, 12)
Find the length diagonal of a rectangle whose length is 35 cm and breadth is 12 cm.
The top of a ladder of length 15 m reaches a window 9 m above the ground. What is the distance between the base of the wall and that of the ladder?
The sides of the triangle are given below. Find out which one is the right-angled triangle?
1.5, 1.6, 1.7
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AB2 + AC2 = 2AD2 + `(1)/(2)"BC"^2`
In a right-angled triangle ABC,ABC = 90°, AC = 10 cm, BC = 6 cm and BC produced to D such CD = 9 cm. Find the length of AD.
If in a ΔPQR, PR2 = PQ2 + QR2, then the right angle of ∆PQR is at the vertex ________
In ∆PQR, PD ⊥ QR such that D lies on QR. If PQ = a, PR = b, QD = c and DR = d, prove that (a + b)(a – b) = (c + d)(c – d).
