Advertisements
Advertisements
प्रश्न
In ∆PQR, PD ⊥ QR such that D lies on QR. If PQ = a, PR = b, QD = c and DR = d, prove that (a + b)(a – b) = (c + d)(c – d).
उत्तर
Given: In ∆PQR,
PD ⊥ QR,
PQ = a,
PR = b,
QD = c
And DR = d
To prove: (a + b)(a – b) = (c + d)(c – d)
Proof: In right angled ΔPDQ,
PQ2 = PD2 + QD2 ...[By pythagoras theorem]
⇒ a2 = PD2 + c2
⇒ PD2 = a2 – c2 ...(i)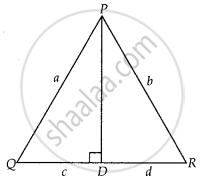
In right angled ∆PDR,
PR2 = PD2 + DR2 ...[By pythagoras theorem]
⇒ b2 = PD2 + d2
⇒ PD2 = b2 – d2 ...(ii)
From equations (i) and (ii),
a2 – c2 = b2 – d2
⇒ a2 – b2 = c2 – d2
⇒ (a – b)(a + b) = (c – d)(c + d)
Hence proved.
APPEARS IN
संबंधित प्रश्न
In a right triangle ABC right-angled at C, P and Q are the points on the sides CA and CB respectively, which divide these sides in the ratio 2 : 1. Prove that
`(i) 9 AQ^2 = 9 AC^2 + 4 BC^2`
`(ii) 9 BP^2 = 9 BC^2 + 4 AC^2`
`(iii) 9 (AQ^2 + BP^2 ) = 13 AB^2`
ABC is an equilateral triangle of side 2a. Find each of its altitudes.
In the given figure, ∠DFE = 90°, FG ⊥ ED, If GD = 8, FG = 12, find (1) EG (2) FD and (3) EF

In the given figure, M is the midpoint of QR. ∠PRQ = 90°. Prove that, PQ2 = 4PM2 – 3PR2.

In ∆ABC, ∠BAC = 90°, seg BL and seg CM are medians of ∆ABC. Then prove that:
4(BL2 + CM2) = 5 BC2

In triangle ABC, AB = AC and BD is perpendicular to AC.
Prove that: BD2 - CD2 = 2CD × AD
In figure AB = BC and AD is perpendicular to CD.
Prove that: AC2 = 2BC. DC.
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AB2 + AC2 = 2AD2 + `(1)/(2)"BC"^2`
Find the length of the support cable required to support the tower with the floor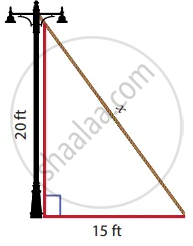
Lengths of sides of a triangle are 3 cm, 4 cm and 5 cm. The triangle is ______.
