Advertisements
Advertisements
प्रश्न
In a quadrilateral ABCD, ∠A + ∠D = 90°. Prove that AC2 + BD2 = AD2 + BC2
[Hint: Produce AB and DC to meet at E.]
उत्तर
Given: Quadrilateral ABCD, in which ∠A + ∠D = 90°
To prove: AC2 + BD2 = AD2 + BC2
Construct: Produce AB and CD to meet at E
Also join AC and BD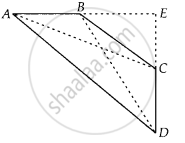
Proof: In ∆AED, ∠A + ∠D = 90° ...[Given]
∴ ∠E = 180° – (∠A + ∠D) = 90° ...[∵ Sum of angles of a triangle = 180°]
Then, by Pythagoras theorem,
AD2 = AE2 + DE2
In ∆BEC, by Pythagoras theorem,
BC2 = BE2 + EC2
On adding both equations, we get
AD2 + BC2 = AE2 + DE2 + BE2 + CE2 ...(i)
In ∆AEC, by Pythagoras theorem,
AC2 = AE2 + CE2
And in ∆BED, by Pythagoras theorem,
BD2 = BE2 + DE2
On adding both equations, we get
AC2 + BD2 = AE2 + CE2 + BE2 + DE2 ...(ii)
From equations (i) and (ii),
AC2 + BD2 = AD2 + BC2
Hence proved.
APPEARS IN
संबंधित प्रश्न
In figure, ∠B of ∆ABC is an acute angle and AD ⊥ BC, prove that AC2 = AB2 + BC2 – 2BC × BD
ABC is a right-angled triangle, right-angled at A. A circle is inscribed in it. The lengths of the two sides containing the right angle are 5 cm and 12 cm. Find the radius of the circle
In a right triangle ABC right-angled at C, P and Q are the points on the sides CA and CB respectively, which divide these sides in the ratio 2 : 1. Prove that
`(i) 9 AQ^2 = 9 AC^2 + 4 BC^2`
`(ii) 9 BP^2 = 9 BC^2 + 4 AC^2`
`(iii) 9 (AQ^2 + BP^2 ) = 13 AB^2`
In triangle ABC, ∠B = 90o and D is the mid-point of BC.
Prove that: AC2 = AD2 + 3CD2.
Prove that `(sin θ + cosec θ)^2 + (cos θ + sec θ)^2 = 7 + tan^2 θ + cot^2 θ`.
In ∆ ABC, AD ⊥ BC.
Prove that AC2 = AB2 +BC2 − 2BC x BD
In the figure, find AR
In ΔABC, if DE || BC, AD = x, DB = x – 2, AE = x + 2 and EC = x – 1, then value of x is ______.
A 5 m long ladder is placed leaning towards a vertical wall such that it reaches the wall at a point 4 m high. If the foot of the ladder is moved 1.6 m towards the wall, then find the distance by which the top of the ladder would slide upwards on the wall.
A right-angled triangle may have all sides equal.
