Advertisements
Advertisements
प्रश्न
In triangle ABC, ∠C=90°. Let BC= a, CA= b, AB= c and let 'p' be the length of the perpendicular from 'C' on AB, prove that:
1. cp = ab
2. `1/p^2=1/a^2+1/b^2`
उत्तर
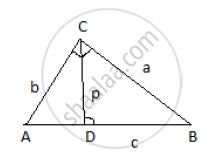
1. Area of a triangle = (1/2) x Base x Height
A(ΔABC) = (1/2) x AB x CD
A(ΔABC) = (1/2) x cp .......(i)
Area of right angle triangle ABC = A(ΔABC) = (1/2) x AC x BC
A(ΔABC) = (1/2) x ba ........(ii)
From (i) and (ii)
cp=ba⇒ cp⇒ab ..........(iii)
2. We have,
cp=ab ..........From(iii)
p = ab/c
Square both sides of the equation.
We get, `p^2=(a^2b^2)/c^2`
`1/p^2=c^2/(a^2b^2)" ..................(iv).....[By invertendo]"`
In right angled triangle ABC,
AB2 = AC2 + BC2 ................[By Pythagoras’ theorem]
c2 = b2 + a2 ............(v)
`c^2/(a^2b^2) = b^2/(a^2b^2) + a^2/(a^2b^2)`..........[Dividing throughout by `a^2b^2`]
`c^2/(ab)^2 = 1/a^2 + 1/b^2` .........(iii)
`c^2/(cp)^2 = 1/a^2 + 1/b^2` ...........[From (ii) and (iii)]
`c^2/(c^2p^2) = 1/a^2 + 1/b^2`
`1/p^2 = 1/a^2 + 1/b^2`
APPEARS IN
संबंधित प्रश्न
In Fig., ∆ABC is an obtuse triangle, obtuse angled at B. If AD ⊥ CB, prove that AC2 = AB2 + BC2 + 2BC × BD
Tick the correct answer and justify: In ΔABC, AB = `6sqrt3` cm, AC = 12 cm and BC = 6 cm.
The angle B is:
In ∆ABC, seg AD ⊥ seg BC, DB = 3CD.
Prove that: 2AB2 = 2AC2 + BC2

In the figure, given below, AD ⊥ BC.
Prove that: c2 = a2 + b2 - 2ax.
ABC is a triangle, right-angled at B. M is a point on BC.
Prove that: AM2 + BC2 = AC2 + BM2
In a quadrilateral ABCD, ∠B = 90° and ∠D = 90°.
Prove that: 2AC2 - AB2 = BC2 + CD2 + DA2
Find the side of the square whose diagonal is `16sqrt(2)` cm.
The sides of a certain triangle is given below. Find, which of them is right-triangle
6 m, 9 m, and 13 m
A boy first goes 5 m due north and then 12 m due east. Find the distance between the initial and the final position of the boy.
The sides of the triangle are given below. Find out which one is the right-angled triangle?
8, 15, 17
In a triangle ABC right angled at C, P and Q are points of sides CA and CB respectively, which divide these sides the ratio 2 : 1.
Prove that: 9AQ2 = 9AC2 + 4BC2
A man goes 18 m due east and then 24 m due north. Find the distance of his current position from the starting point?
The perpendicular PS on the base QR of a ∆PQR intersects QR at S, such that QS = 3 SR. Prove that 2PQ2 = 2PR2 + QR2
A 5 m long ladder is placed leaning towards a vertical wall such that it reaches the wall at a point 4 m high. If the foot of the ladder is moved 1.6 m towards the wall, then find the distance by which the top of the ladder would slide upwards on the wall.
A flag pole 18 m high casts a shadow 9.6 m long. Find the distance of the top of the pole from the far end of the shadow.
In figure, PQR is a right triangle right angled at Q and QS ⊥ PR. If PQ = 6 cm and PS = 4 cm, find QS, RS and QR.
Height of a pole is 8 m. Find the length of rope tied with its top from a point on the ground at a distance of 6 m from its bottom.
Points A and B are on the opposite edges of a pond as shown in figure. To find the distance between the two points, the surveyor makes a right-angled triangle as shown. Find the distance AB.

