Advertisements
Advertisements
प्रश्न
The perpendicular PS on the base QR of a ∆PQR intersects QR at S, such that QS = 3 SR. Prove that 2PQ2 = 2PR2 + QR2
उत्तर
Given QS = 3SR
QR = QS + SR
= 3SR + SR = 4SR
SR = `1/4` QR ...(1)
QS = 3SR
SR = `"QS"/3` ...(2)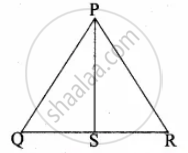
From (1) and (2) we get
`1/4 "QR" = "QS"/3`
∴ QS = `3/4` QR ...(3)
In the right ∆PQS,
PQ2 = PS2 + QS2 ...(4)
Similarly in ∆PSR
PR2 = PS2 + SR2 ...(5)
Subtract (4) and (5)
PQ2 – PR2 = PS2 + QS2 – PS2 – SR2
= QS2 – SR2
PQ2 – PR2 = `[3/4 "QR"]^2 - ["QR"/4]^2`
From (3) and (1)
= `(9"QR"^2)/16 - "QR"^2/16`
= `(8"QR"^2)/16`
PQ2 – PR2 = `1/2 "QR"^2`
2PQ2 – 2PR2 = QR2
2PQ2 = 2PR2 + QR2
Hence the proved.
APPEARS IN
संबंधित प्रश्न
The points A(4, 7), B(p, 3) and C(7, 3) are the vertices of a right traingle ,right-angled at B. Find the values of p.
P and Q are the mid-points of the sides CA and CB respectively of a ∆ABC, right angled at C. Prove that:
`(i) 4AQ^2 = 4AC^2 + BC^2`
`(ii) 4BP^2 = 4BC^2 + AC^2`
`(iii) (4AQ^2 + BP^2 ) = 5AB^2`
In the given figure, AD is a median of a triangle ABC and AM ⊥ BC. Prove that:

`"AC"^2 = "AD"^2 + "BC"."DM" + (("BC")/2)^2`
Identify, with reason, if the following is a Pythagorean triplet.
(3, 5, 4)
A point OI in the interior of a rectangle ABCD is joined with each of the vertices A, B, C and D. Prove that OB2 + OD2 = OC2 + OA2
From the given figure, in ∆ABQ, if AQ = 8 cm, then AB =?

The perimeters of two similar triangles ABC and PQR are 60 cm and 36 cm respectively. If PQ = 9 cm, then AB equals ______.
If ΔABC ~ ΔPQR, `("ar" triangle "ABC")/("ar" triangle "PQR") = 9/4` and AB = 18 cm, then the length of PQ is ______.
The longest side of a right angled triangle is called its ______.
Two squares having same perimeter are congruent.
