Advertisements
Advertisements
प्रश्न
A point OI in the interior of a rectangle ABCD is joined with each of the vertices A, B, C and D. Prove that OB2 + OD2 = OC2 + OA2
उत्तर
Let ABCD be the given rectangle and let O be a point within it.
Join OA, OB, OC and OD.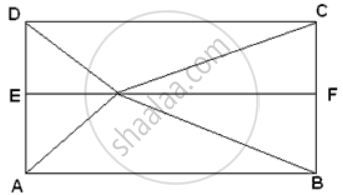
Through O, draw EOF || AB. Then, ABFE is a rectangle.
In right triangles ΔOEA and ΔOFC, we have
OA2 = OE2 + AE2 and OC2 = OF2 + CF2
⇒ OA2 + OC2 = (OE2 + AE2) + (OF2 + CF2)
⇒ OA2 + OC2 = OE2 + OF2 + AE2 + CF2 ......(i)
Now, in right triangles OFB and ODE, we have
OB2 = OF2 + FB2 and OD2 = OE2 + DE2
⇒ OB2 + OD2 = (OF2 + FB2) + (OE2 + DE2)
⇒ OB2 + OD2 = OE2 + OF2 + DE2 + BF2
⇒ OB2 + OD2 = OE2 + OF2 + CF2 + AE2 [∵ DE = CF and AE = BF]....(ii)
From (i) and (ii), we get
OA2 + OC2 = OB2 + OD2.
APPEARS IN
संबंधित प्रश्न
ABC is an isosceles triangle with AC = BC. If AB2 = 2AC2, prove that ABC is a right triangle.
In the given figure, AD is a median of a triangle ABC and AM ⊥ BC. Prove that:

`"AC"^2 = "AD"^2 + "BC"."DM" + (("BC")/2)^2`
Prove that the sum of the squares of the diagonals of parallelogram is equal to the sum of the squares of its sides.
In an isosceles triangle, length of the congruent sides is 13 cm and its base is 10 cm. Find the distance between the vertex opposite the base and the centroid.
In the given figure, ∠B = 90°, XY || BC, AB = 12 cm, AY = 8cm and AX : XB = 1 : 2 = AY : YC.
Find the lengths of AC and BC.

In an isosceles triangle ABC; AB = AC and D is the point on BC produced.
Prove that: AD2 = AC2 + BD.CD.
Prove that `(sin θ + cosec θ)^2 + (cos θ + sec θ)^2 = 7 + tan^2 θ + cot^2 θ`.
Prove that (1 + cot A - cosec A ) (1 + tan A + sec A) = 2
In ∆ ABC, AD ⊥ BC.
Prove that AC2 = AB2 +BC2 − 2BC x BD
The sides of a certain triangle is given below. Find, which of them is right-triangle
6 m, 9 m, and 13 m
In the figure below, find the value of 'x'.
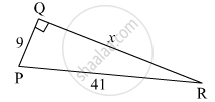
In the right-angled ∆PQR, ∠ P = 90°. If l(PQ) = 24 cm and l(PR) = 10 cm, find the length of seg QR.
Find the Pythagorean triplet from among the following set of numbers.
2, 4, 5
The sides of the triangle are given below. Find out which one is the right-angled triangle?
40, 20, 30
Two poles of height 9m and 14m stand on a plane ground. If the distance between their 12m, find the distance between their tops.
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AB2 + AC2 = 2AD2 + `(1)/(2)"BC"^2`
∆ABC is right-angled at C. If AC = 5 cm and BC = 12 cm. find the length of AB.
Sides AB and BE of a right triangle, right-angled at B are of lengths 16 cm and 8 cm respectively. The length of the side of largest square FDGB that can be inscribed in the triangle ABE is ______.

If S is a point on side PQ of a ΔPQR such that PS = QS = RS, then ______.
Jiya walks 6 km due east and then 8 km due north. How far is she from her starting place?
