Advertisements
Advertisements
प्रश्न
In the figure below, find the value of 'x'.
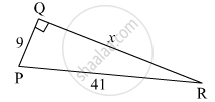
उत्तर

In the right-angled triangle PQR,
∠Q = 90°
Hence, side PR is the hypotenuse.
According to Pythagoras' theorem,
l(PR)2 = l(QR)2 + l(PQ)2
⇒ (41)2 = (x)2 + (9)2
⇒ 1681 = x2 + 81
⇒ x2 = 1681 − 81
⇒ x2 = 1600
⇒ x2 = (40)2
⇒ x = 40
∴ The value of x is 40.
संबंधित प्रश्न
In the following figure, O is a point in the interior of a triangle ABC, OD ⊥ BC, OE ⊥ AC and OF ⊥ AB. Show that

(i) OA2 + OB2 + OC2 − OD2 − OE2 − OF2 = AF2 + BD2 + CE2
(ii) AF2 + BD2 + CE2 = AE2 + CD2 + BF2
In the given figure, ∆ABC is an equilateral triangle of side 3 units. Find the coordinates of the other two vertices ?

In an isosceles triangle, length of the congruent sides is 13 cm and its base is 10 cm. Find the distance between the vertex opposite the base and the centroid.
In triangle ABC, AB = AC and BD is perpendicular to AC.
Prove that: BD2 - CD2 = 2CD × AD
ABC is a triangle, right-angled at B. M is a point on BC.
Prove that: AM2 + BC2 = AC2 + BM2
Find the Pythagorean triplet from among the following set of numbers.
4, 7, 8
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AB2 + AC2 = 2AD2 + `(1)/(2)"BC"^2`
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AC2 - AB2 = 2BC x ED
Lengths of sides of a triangle are 3 cm, 4 cm and 5 cm. The triangle is ______.
The top of a broken tree touches the ground at a distance of 12 m from its base. If the tree is broken at a height of 5 m from the ground then the actual height of the tree is ______.
