Advertisements
Advertisements
प्रश्न
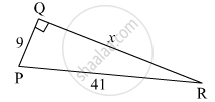
In the figure below, find the value of 'x'.
उत्तर

In the right-angled triangle PQR,
∠Q = 90°
Hence, side PR is the hypotenuse.
According to Pythagoras' theorem,
l(PR)2 = l(QR)2 + l(PQ)2
⇒ (41)2 = (x)2 + (9)2
⇒ 1681 = x2 + 81
⇒ x2 = 1681 − 81
⇒ x2 = 1600
⇒ x2 = (40)2
⇒ x = 40
∴ The value of x is 40.
संबंधित प्रश्न
The diagonal of a rectangular field is 16 metres more than the shorter side. If the longer side is 14 metres more than the shorter side, then find the lengths of the sides of the field.
In Figure, ABD is a triangle right angled at A and AC ⊥ BD. Show that AD2 = BD × CD

In a trapezium ABCD, seg AB || seg DC seg BD ⊥ seg AD, seg AC ⊥ seg BC, If AD = 15, BC = 15 and AB = 25. Find A(▢ABCD)

In triangle ABC, AB = AC = x, BC = 10 cm and the area of the triangle is 60 cm2.
Find x.
In equilateral Δ ABC, AD ⊥ BC and BC = x cm. Find, in terms of x, the length of AD.
In Fig. 3, ∠ACB = 90° and CD ⊥ AB, prove that CD2 = BD x AD.

Find the Pythagorean triplet from among the following set of numbers.
4, 7, 8
In a right-angled triangle ABC,ABC = 90°, AC = 10 cm, BC = 6 cm and BC produced to D such CD = 9 cm. Find the length of AD.
In a right-angled triangle PQR, right-angled at Q, S and T are points on PQ and QR respectively such as PT = SR = 13 cm, QT = 5 cm and PS = TR. Find the length of PQ and PS.
A right-angled triangle may have all sides equal.
