Advertisements
Advertisements
Question
In the figure below, find the value of 'x'.
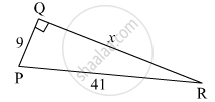
Solution

In the right-angled triangle PQR,
∠Q = 90°
Hence, side PR is the hypotenuse.
According to Pythagoras' theorem,
l(PR)2 = l(QR)2 + l(PQ)2
⇒ (41)2 = (x)2 + (9)2
⇒ 1681 = x2 + 81
⇒ x2 = 1681 − 81
⇒ x2 = 1600
⇒ x2 = (40)2
⇒ x = 40
∴ The value of x is 40.
RELATED QUESTIONS
If ABC is an equilateral triangle of side a, prove that its altitude = ` \frac { \sqrt { 3 } }{ 2 } a`
Two poles of heights 6 m and 11 m stand on a plane ground. If the distance between the feet of the poles is 12 m, find the distance between their tops.
In the following figure, AD is perpendicular to BC and D divides BC in the ratio 1: 3.
Prove that : 2AC2 = 2AB2 + BC2
Find the value of (sin2 33 + sin2 57°)
Prove that `(sin θ + cosec θ)^2 + (cos θ + sec θ)^2 = 7 + tan^2 θ + cot^2 θ`.
Triangle PQR is right-angled at vertex R. Calculate the length of PR, if: PQ = 34 cm and QR = 33.6 cm.
In the given figure, angle BAC = 90°, AC = 400 m, and AB = 300 m. Find the length of BC.

In the given figure, angle ADB = 90°, AC = AB = 26 cm and BD = DC. If the length of AD = 24 cm; find the length of BC.

Each side of rhombus is 10cm. If one of its diagonals is 16cm, find the length of the other diagonals.
Prove that the area of the equilateral triangle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the equilateral triangles drawn on the other two sides of the triangle.
