Advertisements
Advertisements
प्रश्न
Jiya walks 6 km due east and then 8 km due north. How far is she from her starting place?
उत्तर
Let A be the starting point and B be the ending point of Jiya.
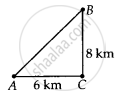
Since ∆ABC is right-angled.
∴ (AB)2 = (AC)2 + (BC)2
⇒ (AB)2 = 62 + 82
= 36 + 64
= 100
⇒ AB = 10
Thus, Jiya is 10 km away from her starting place.
APPEARS IN
संबंधित प्रश्न
From a point O in the interior of a ∆ABC, perpendicular OD, OE and OF are drawn to the sides BC, CA and AB respectively. Prove
that :
`(i) AF^2 + BD^2 + CE^2 = OA^2 + OB^2 + OC^2 – OD^2 – OE^2 – OF^2`
`(ii) AF^2 + BD^2 + CE^2 = AE^2 + CD^2 + BF^2`
ABC is a right triangle right-angled at C. Let BC = a, CA = b, AB = c and let p be the length of perpendicular from C on AB, prove that
(i) cp = ab
`(ii) 1/p^2=1/a^2+1/b^2`
Sides of triangle are given below. Determine it is a right triangle or not? In case of a right triangle, write the length of its hypotenuse. 13 cm, 12 cm, 5 cm
Find the length diagonal of a rectangle whose length is 35 cm and breadth is 12 cm.

In ΔMNP, ∠MNP = 90˚, seg NQ ⊥ seg MP, MQ = 9, QP = 4, find NQ.
In the following figure, AD is perpendicular to BC and D divides BC in the ratio 1: 3.
Prove that : 2AC2 = 2AB2 + BC2
In an isosceles triangle ABC; AB = AC and D is the point on BC produced.
Prove that: AD2 = AC2 + BD.CD.
Find the Pythagorean triplet from among the following set of numbers.
4, 7, 8
A man goes 10 m due east and then 24 m due north. Find the distance from the straight point.
Two trees 7 m and 4 m high stand upright on a ground. If their bases (roots) are 4 m apart, then the distance between their tops is ______.
