Advertisements
Advertisements
प्रश्न
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AB2 + AC2 = 2(AD2 + CD2)
उत्तर
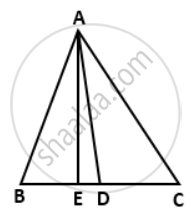
We have ∠AED = 90°
∴ ∠ADE < 90° and ∠ADC > 90°
i.e. ∠ADE is acute and ∠ADC is obtuse.
From (iii), we have
AB2 + AC2 = `2"AD"^2 + (1)/(2)"BC"^2`
⇒ AB2 + AC2 = `2"AD"^2 + (1)/(2)(2 xx "CD")^2`
⇒ AB2 + AC2 = `2"AD"^2 + (1)/(2) xx 4"CD"^2`
⇒ AB2 + AC2 = 2AD2 + 2CD2
⇒ AB2 + AC2 = 2(AD2 + CD2).
APPEARS IN
संबंधित प्रश्न
In a right triangle ABC, right-angled at B, BC = 12 cm and AB = 5 cm. The radius of the circle inscribed in the triangle (in cm) is
(A) 4
(B) 3
(C) 2
(D) 1
From a point O in the interior of a ∆ABC, perpendicular OD, OE and OF are drawn to the sides BC, CA and AB respectively. Prove
that :
`(i) AF^2 + BD^2 + CE^2 = OA^2 + OB^2 + OC^2 – OD^2 – OE^2 – OF^2`
`(ii) AF^2 + BD^2 + CE^2 = AE^2 + CD^2 + BF^2`
A 15 m long ladder reached a window 12 m high from the ground on placing it against a wall at a distance a. Find the distance of the foot of the ladder from the wall.

Some question and their alternative answer are given. Select the correct alternative.
If a, b, and c are sides of a triangle and a2 + b2 = c2, name the type of triangle.

In ΔMNP, ∠MNP = 90˚, seg NQ ⊥ seg MP, MQ = 9, QP = 4, find NQ.
A man goes 40 m due north and then 50 m due west. Find his distance from the starting point.
If P and Q are the points on side CA and CB respectively of ΔABC, right angled at C, prove that (AQ2 + BP2 ) = (AB2 + PQ2)
Triangle ABC is right-angled at vertex A. Calculate the length of BC, if AB = 18 cm and AC = 24 cm.
The sides of a certain triangle is given below. Find, which of them is right-triangle
16 cm, 20 cm, and 12 cm
A boy first goes 5 m due north and then 12 m due east. Find the distance between the initial and the final position of the boy.
PQR is an isosceles triangle with PQ = PR = 10 cm and QR = 12 cm. Find the length of the perpendicular from P to QR.
∆ABC is right-angled at C. If AC = 5 cm and BC = 12 cm. find the length of AB.
In triangle ABC, line I, is a perpendicular bisector of BC.
If BC = 12 cm, SM = 8 cm, find CS
Choose the correct alternative:
If length of sides of a triangle are a, b, c and a2 + b2 = c2, then which type of triangle it is?
If S is a point on side PQ of a ΔPQR such that PS = QS = RS, then ______.
Prove that the area of the semicircle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the semicircles drawn on the other two sides of the triangle.
The perimeter of the rectangle whose length is 60 cm and a diagonal is 61 cm is ______.
The longest side of a right angled triangle is called its ______.
If the hypotenuse of one right triangle is equal to the hypotenuse of another right triangle, then the triangles are congruent.
Two poles of 10 m and 15 m stand upright on a plane ground. If the distance between the tops is 13 m, find the distance between their feet.
